《2025年长江作业本同步练习册九年级数学上册人教版》

1. 如图,圆锥形冰淇淋盒的母线长是13 cm,高是12 cm,则该圆锥形底面圆的面积是( )

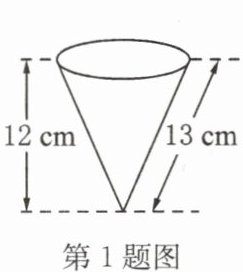
A.$10π\ cm^2$
B.$25π\ cm^2$
C.$60π\ cm^2$
D.$65π\ cm^2$

答案： B

2. 如图,$⊙O$中,半径$OA = 4$,$∠AOB = 120^{\circ}$,用阴影部分的扇形围成的圆锥底面圆的半径长是( )

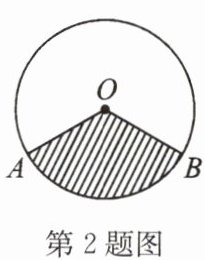
A.1
B.$\frac{4}{3}$
C.$\frac{5}{3}$
D.2

答案： B

3. 如图,在$3×3$的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中的圆弧为格点$\triangle ABC$外接圆的一部分,若小正方形的边长为1,则图中阴影部分的面积为( )

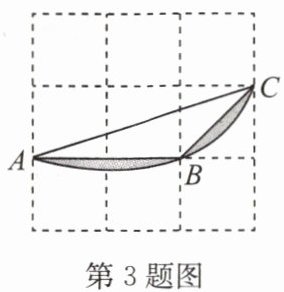
A.$\frac{5}{2}π - \frac{7}{4}$
B.$\frac{5}{2}π - \frac{7}{2}$
C.$\frac{5}{4}π - \frac{7}{4}$
D.$\frac{5}{4}π - \frac{7}{2}$

答案： D

4. 沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”. 如图,$\overset{\frown}{AB}是以O$为圆心、$OA$为半径的圆弧,$C是弦AB$的中点,$D在\overset{\frown}{AB}$上,$CD⊥AB$. “会圆术”给出了$\overset{\frown}{AB}的长l的近似值s$的计算公式：$s = AB + \frac{CD^2}{OA}$,那么,当$OA = 2$,$∠AOB = 90^{\circ}$时,$|l - s| = $______.(结果保留一位小数)

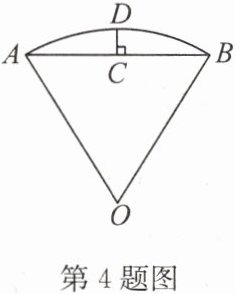
答案： 0.1

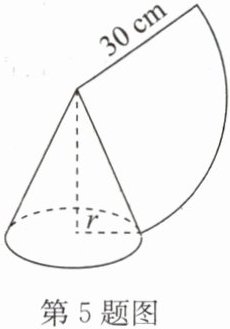
5. 如图,用一个半径为30 cm,面积为$300π\ cm^2$的扇形铁皮,制作一个无底的圆锥(不计损耗).
(1)求扇形的圆心角的度数；
(2)求圆锥的底面半径$r$.

答案：
(1)120°;
(2)10 cm

6. 如图,一个直角三角形两条直角边分别为3 cm和4 cm,以斜边$AB$所在直线为轴旋转一周得到一个几何体,在虚线框内画出这个几何体的草图,求这个几何体的表面积.

答案： 图略,$\frac{84}{5}\pi$