《2025年学习之友八年级数学上册北师大版》

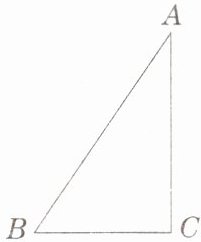
9. 一旗杆高 $ 10 \mathrm{m} $,旗杆顶部 A 与地面一固定点 B 之间要拉一笔直的铁索,已知固定点 B 到旗杆底部的距离是 $ 7 \mathrm{m} $,一个工人准备了长约 $ 12.5 \mathrm{m} $ 的铁索,你认为这一长度够吗？
]

答案： 在直角三角形$ABC$中，旗杆高度$AC$为直角边，长度为$10m$，固定点$B$到旗杆底部的距离$BC$为另一直角边，长度为$7m$。
根据勾股定理，斜边$AB$（即铁索的长度）的平方等于两直角边的平方和，即：
$AB^2 = AC^2 + BC^2$。
代入已知数值：
$AB^2 = 10^2 + 7^2 = 100 + 49 = 149$。
对149开平方得到铁索的长度：
$AB = \sqrt{149} \approx 12.2 (m)$（结果保留一位小数）。
由于$12.2 m ＜ 12.5m$，
因此，长度为$12.5m$的铁索足够使用。

1. 下列各数与 $ \sqrt{7} $ 最接近的是(B)。
A.2.5
B.2.6
C.2.7
D.2.8

答案： B

2. 如图,数轴上点 N 表示的数可能是(A)。

A.$ \sqrt{10} $
B.$ \sqrt{5} $
C.$ \sqrt{3} $
D.$ \sqrt{2} $

答案： A

3. 设 $ \sqrt{26}= a $,则下列结论正确的是(B)。
A.$ 4.5 ＜ a ＜ 5.0 $
B.$ 5.0 ＜ a ＜ 5.5 $
C.$ 5.5 ＜ a ＜ 6.0 $
D.$ 6.0 ＜ a ＜ 6.5 $

答案： B

4. 一个正方体的体积为 $ 28360 \mathrm{cm}^3 $,正方体的棱长估计为(C)。
A.$ 22 \mathrm{cm} $
B.$ 27 \mathrm{cm} $
C.$ 30.5 \mathrm{cm} $
D.$ 40 \mathrm{cm} $

答案： C

5. 利用计算器求下列各式的值：(结果精确到 0.001)
(1) $ \sqrt{83} \approx $9.110；
(2) $ -\sqrt{3.28} \approx $-1.811；
(3) $ \sqrt[3]{-0.789} \approx $-0.924；
(4) $ \sqrt[3]{83} \approx $4.362；
(5) $ \sqrt{10}+2.23-\pi \approx $2.251；
(6) $ (-4) × \sqrt{7}+2 \sqrt{6} \approx $-5.684。

答案： 9.110；-1.811；-0.924；4.362；2.251；-5.684

6. 下列计算结果是否正确？说明理由。
(1) $ \sqrt{2430} \approx 9.8 $；
(2) $ \sqrt[3]{983000} \approx 125 $；
(3) $ \sqrt[3]{890} \approx 95 $；
(4) $ \sqrt{0.35} \approx 0.6 $。

答案：
(1) 不正确。理由：因为 $9.8^2 = 96.04$，而 $96.04 \ll 2430$，所以 $\sqrt{2430} \approx 9.8$ 错误。
(2) 不正确。理由：因为 $125^3 = 1953125$，而 $1953125 \gg 983000$，所以 $\sqrt[3]{983000} \approx 125$ 错误。
(3) 不正确。理由：因为 $95^3 = 857375$，而 $857375 \gg 890$，所以 $\sqrt[3]{890} \approx 95$ 错误。
(4) 不正确。理由：因为 $0.6^2 = 0.36$，而 $0.36 \approx 0.35$ 但不够精确，更接近的是 $\sqrt{0.35} \approx 0.5916$，所以 $\sqrt{0.35} \approx 0.6$ 错误。

7. 通过估算比较大小：
(1) $ \sqrt{17} $ 与 4.3；
(2) $ -3.7 $ 与 $ -\sqrt{11} $；
(3) $ \sqrt[3]{9} $ 与 2.1；
(4) $ -\sqrt[3]{65} $ 与 -4；
(5) $ \frac{\sqrt[3]{9}-1}{3} $ 与 $ \frac{2}{3} $；
(6) $ \frac{\sqrt{15}-1}{8} $ 与 $ \frac{3}{8} $。

答案：
(1) 因为$4.3^2 = 18.49$，$17 ＜ 18.49$，所以$\sqrt{17} ＜ 4.3$。
(2) 因为$3.7^2 = 13.69$，$13.69 ＞ 11$，所以$3.7 ＞ \sqrt{11}$，故$-3.7 ＜ -\sqrt{11}$。
(3) 因为$2.1^3 = 9.261$，$9 ＜ 9.261$，所以$\sqrt[3]{9} ＜ 2.1$。
(4) 因为$4^3 = 64$，$65 ＞ 64$，所以$\sqrt[3]{65} ＞ 4$，故$-\sqrt[3]{65} ＜ -4$。
(5) 因为$\sqrt[3]{9} ＜ 3$，所以$\sqrt[3]{9} - 1 ＜ 2$，两边同除以3得$\frac{\sqrt[3]{9}-1}{3} ＜ \frac{2}{3}$。
(6) 因为$\sqrt{15} ＜ 4$，所以$\sqrt{15} - 1 ＜ 3$，两边同除以8得$\frac{\sqrt{15}-1}{8} ＜ \frac{3}{8}$。