《2025年学习之友八年级数学上册北师大版》

1. 各个数据与平均数差的平方的平均数称为方差,用$ s^{2} $表示。

答案： 方差 $ s^{2} $

2. 一组数据的方差或标准差越小,这组数据就越稳定,数据的离散程度可以用方差、标准差刻画。

答案： 方差 方差 标准差

3. 已知一组数据的方差是3,则这组数据的标准差是$ \sqrt{3} $。

答案： $ \sqrt{3} $

4. 一组数据4,3,6,x的平均数是4,则这组数据的标准差是$ \frac{\sqrt{6}}{2} $。

答案： $ \frac{\sqrt{6}}{2} $

5. 若数据x,2x,3x,4x,5x的平均数是6,则x= 2,方差$s^2= $_________8,标准差为_________$ 2\sqrt{2} $。

答案： 2 8 $ 2\sqrt{2} $

6. 甲、乙两班举行班级电脑汉字输入比赛,各选10名选手参赛,各班参赛学生每分钟输入汉字个数统计如下表：
 

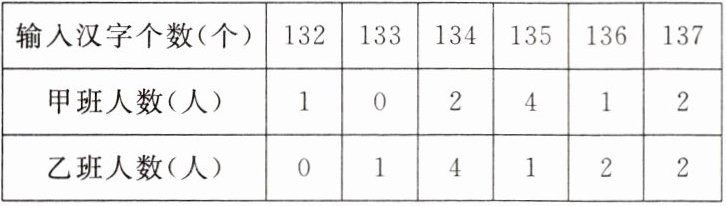
通过计算可知两组数据的方差分别为$s^2₍$甲$₎= 2.0,s^2₍$乙₎= 2.7,则下列说法：① 两组数据的平均数相同；② 甲组学生比乙组学生的成绩稳定。其中正确的说法有①②。(填序号)

答案： ①②

7. 一组数据2,5,5,6,7的方差为(B)。
A.14
B.2.8
C.2.5
D.0

答案： B

8. 某部门四名员工的月工资都为5000元,后来又来了一名新员工,月工资为4800元,这五名员工工资与原来四名员工工资比较,方差(D)。
A.没有变化
B.无法确定
C.变小了
D.变大了

答案： D

9. 若一组数据2,3,4,5,x的方差比另一组数据5,6,7,8,9的方差大,则x的值可能是(B)。
A.1
B.8
C.6
D.4

答案： B

10. 已知一个样本为：0,2,-1,3,-4,则这个样本的方差是(B)。
A.30
B.6
C.$\sqrt{6}$
D.0

答案： B

11. 在这学期的六次体育测试中,甲、乙两同学的平均成绩一样,方差分别为1.5,1.0,则下列说法正确的是(A)。
A.乙同学的成绩更稳定
B.甲同学的成绩更稳定
C.甲、乙两位同学的成绩一样稳定
D.不能确定哪位同学的成绩更稳定

答案： A

1. 某学校从九年级同学中任意选取40人,随机分成甲、乙两个小组(每组20人)进行“引体向上”体能测试,根据测试成绩绘制出下面的统计表和统计图。
甲组成绩统计表
| 


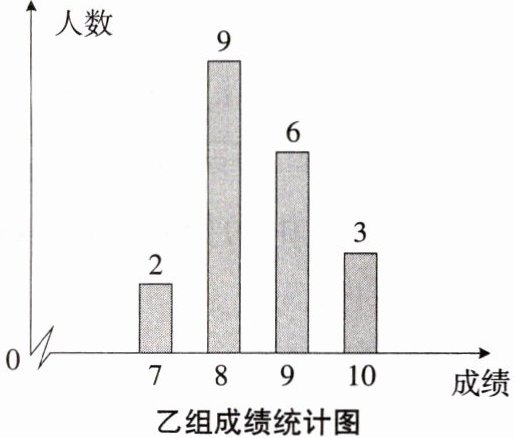
请根据上面的信息,解答下列问题：
(1)请求出乙组成绩的平均数；
(2)已知甲组成绩的方差为$s^2₍$甲₎= 0.81,请求乙组成绩的方差,并判断哪个小组的成绩更加稳定。

答案：
(1)乙组成绩的平均数为$ \frac{1}{20}×(2×7 + 9×8 + 9×6 + 10×3)=8.5 $(分);
(2)乙组的方差是:$ \frac{1}{20}×[2×(7 - 8.5)^{2}+9×(8 - 8.5)^{2}+6×(9 - 8.5)^{2}+3×(10 - 8.5)^{2}]=0.75 $,因为$ s_{乙}^{2}＜s_{甲}^{2} $,所以乙组的成绩更加稳定.