《2025年学习之友八年级数学上册北师大版》

【问题情境】
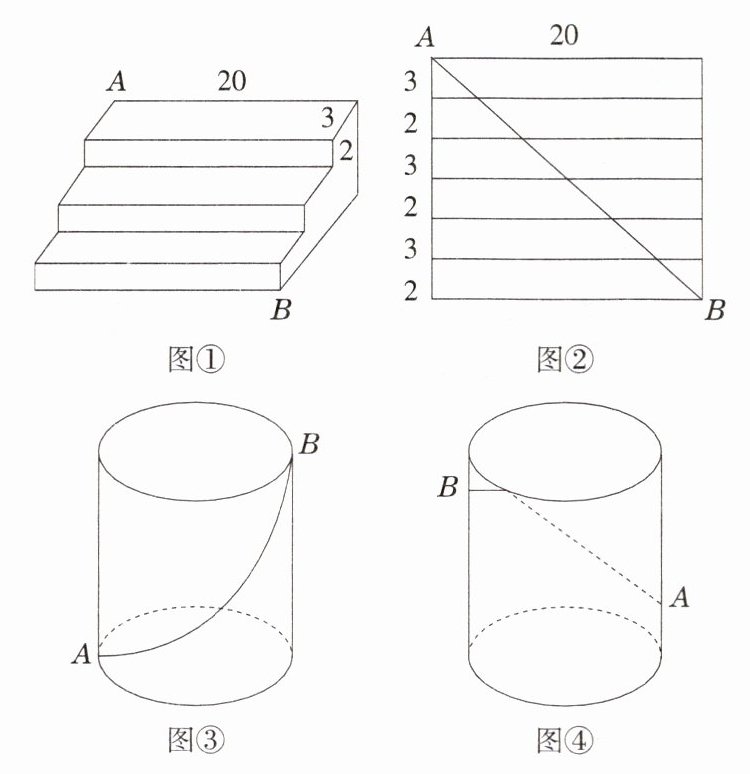
数学综合与实践活动课上,老师提出如下问题：一个三级台阶,它每一级的长、宽、高分别为 $20$、$3$、$2$,$A$ 和 $B$ 是一个台阶两个相对的端点。

【探究实践】
老师让同学们探究：如图 ①,若 $A$ 点处有一只蚂蚁要到 $B$ 点去吃可口的食物,那么蚂蚁沿着台阶爬到 $B$ 点的最短路程是多少？
(1)同学们经过思考得到如下解题方法：如图 ②,将三级台阶展开成平面图形,可得到长为 $20$,宽为 $15$ 的长方形,连接 $AB$,经过计算得到 $AB$ 长度为 ______,就是最短路程。
【变式探究】
(2)如图 ③,是一只圆柱形玻璃杯,该玻璃杯的底面周长是 $30\mathrm{cm}$,高是 $8\mathrm{cm}$,若蚂蚁从点 $A$ 出发沿着玻璃杯的侧面到点 $B$,则蚂蚁爬行的最短距离为 ______。
【拓展应用】
(3)如图 ④,圆柱形玻璃杯的高 $9\mathrm{cm}$,底面周长为 $16\mathrm{cm}$,在杯内壁离杯底 $4\mathrm{cm}$ 的点 $A$ 处有一滴蜂蜜,此时,一只蚂蚁正好在外壁上,离杯上沿 $1\mathrm{cm}$,且与蜂蜜相对的点 $B$ 处,则蚂蚁从外壁 $B$ 处到内壁 $A$ 处所爬行的最短路程是多少？(杯壁厚度不计)

答案：

(1)25
(2)17cm
(3)10cm
解:如图,将玻璃杯侧面展开,作B关于EF的对称点$B'$,作$B'D⊥AE$,交AE延长线于点D,连接$AB'$.由题意得:$DE=\frac {1}{2}BB'=1cm$,$AE=9 - 4=5(cm)$,

所以$AD=AE + DE=6cm$.
因为底面周长为16cm,所以$B'D=\frac {1}{2}×16=8(cm)$,
所以$AB'^{2}=AD^{2}+B'D^{2}=6^{2}+8^{2}=100$,即$AB'=10(cm)$
由两点之间线段最短可知,蚂蚁从外壁B处到内壁A处所走的最短路程为$AB'=10cm$.