《2025年学习之友八年级数学上册北师大版》

2. 高铁的开通,给 $ A $ 市市民的出行带来了极大的方便,五一期间,乐乐和颖颖相约到 $ B $ 市某游乐场游玩. 乐乐乘私家车从 $ A $ 市出发 1 小时后,颖颖乘坐高铁从 $ A $ 市出发,先到 $ B $ 市火车东站,然后转乘出租车到游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开 $ A $ 市的距离 $ y $(千米) 与时间 $ t $(小时) 的关系如下图所示,请结合图象解决下面问题.

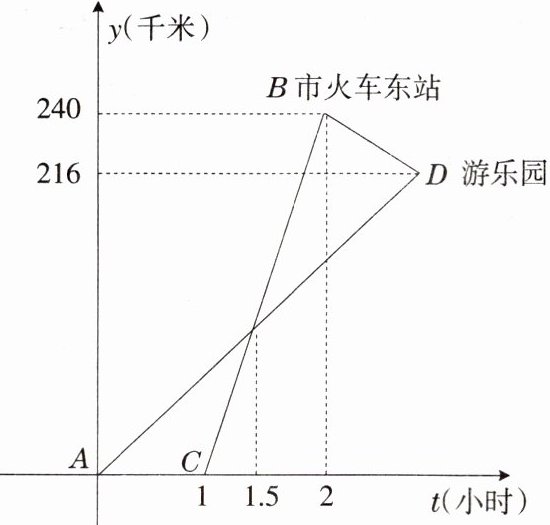
(1) 高铁的平均速度是每小时多少千米?
(2) 当颖颖到达 $ B $ 市火车东站时,乐乐距离游乐园还有多少千米?
(3) 若乐乐要提前 18 分钟到达游乐园,问私家车的速度必须达到多少千米/小时?

答案： 解:
(1)如图所示，v=240/(2-1)=240(千米/小时)　
(2)设直线BC为y=kt+b 　当t=1时,y=0,当t=2时,y=240 　{k+b=02k+b=240 解得{k=240b=-240
∴y=240t−240 　当t=1.5时代入　y=240×1.5−240=120 　设直线OD为y=kt 　当t=1.5时y=120 　120=1.5t　t=80
∴y=80t 　当t=2　y=160 　216−160=56(千米)　
(3)当y=216时代入216=80t 　t=2.7 　2.7−18/60=2.4(小时)　216÷2.4=90(千米/小时)

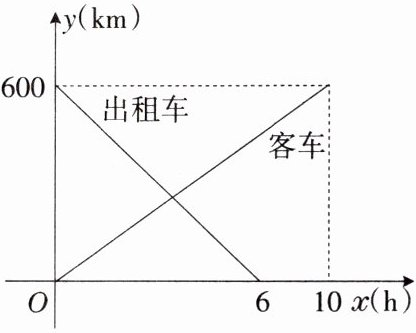
3. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为 $ y_1(km) $,出租车离甲地的距离为 $ y_2(km) $,两车行驶的时间为 $ x(h) $,$ y_1 $,$ y_2 $ 关于 $ x $ 的函数图象如图所示：
(1) 根据图象,直接写出 $ y_1 $,$ y_2 $ 关于 $ x $ 的函数关系式；
(2) 甲、乙两地间有 $ A $,$ B $ 两个加油站,相距 $ 200\ km $,若客车进入 $ A $ 加油站时,出租车恰好进入 $ B $ 加油站,求 $ A $ 加油站离甲地的距离.

答案： 解:
(1)设y₁=kx,将(10,600)代入　600=10k　k=60
∴y₁=60x 　设y₂=kx+600将(6,0)代入　0=6k+600　k=−100
∴y₂=−100x+600 　
(2)①当A加油站在甲地与B加油站之间时,(-100x+600)−60x=200,解得x=2.5此时,A加油站距离甲地:60×2.5=150(km),　②当B加油站在甲地与A加油站之间时,60x−(-100x+600)=200,解得x=5,此时,A加油站距离甲地:60×5=300km,综上所述,A加油站到甲地距离为150km或300km.