《2025年学习之友八年级数学上册北师大版》

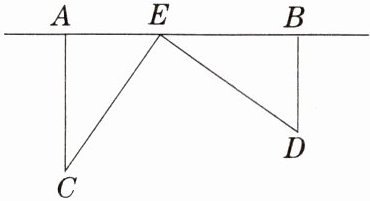
7. 为了丰富少年儿童的业余生活,某社区要在如图所示$AB$所在的直线上建一图书室.该社区有两所学校所在的位置在点$C和点D$处,$CA\perp AB于A$,$DB\perp AB于B$,已知$AB = 25km$,$CA = 15km$,$DB = 10km$,试问：图书室$E应该建在距点A$多少千米处,才能使它到两所学校的距离相等？

答案： 设图书室$E$距点$A$的距离为$x$千米，则$E$距点$B$的距离为$(25 - x)$千米。
因为$CA\perp AB$，$DB\perp AB$，所以$\triangle ACE$和$\triangle BDE$均为直角三角形。
根据勾股定理，$CE^2 = CA^2 + AE^2 = 15^2 + x^2$，$DE^2 = DB^2 + BE^2 = 10^2 + (25 - x)^2$。
由于$CE = DE$，所以$15^2 + x^2 = 10^2 + (25 - x)^2$。
展开得：$225 + x^2 = 100 + 625 - 50x + x^2$。
化简得：$225 = 725 - 50x$。
移项得：$50x = 725 - 225 = 500$。
解得：$x = 10$。
答：图书室$E$应该建在距点$A$10千米处。

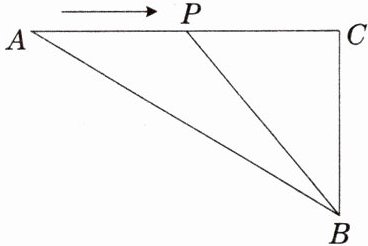
1. 在$\triangle ABC$中,$AB = 50cm$,$BC = 30cm$,$\angle C = 90^{\circ}$,点$P从点A开始沿AC边向点C以2cm/s$的速度移动,则几秒后$\triangle PCB的面积等于300$平方厘米？

答案： 在$\triangle ABC$中，$\angle C = 90°$，$BC = 30cm$，由勾股定理可得：
$AC = \sqrt{AB^2 - BC^2} = \sqrt{50^2 - 30^2} = \sqrt{2500 - 900} = \sqrt{1600} = 40cm$。
设$t$秒后$\triangle PCB$的面积等于$300$平方厘米，此时$AP = 2tcm$，则：
$PC = AC - AP = 40 - 2t$，
$\triangle PCB$的面积公式为：
$S = \frac{1}{2} × PC × BC = \frac{1}{2} × (40 - 2t) × 30 = 300$，
化简方程：
$\frac{1}{2} × (40 - 2t) × 30 = 300$，
$(40 - 2t) × 15 = 300$，
$40 - 2t = 20$，
$2t = 20$，
$t = 10$。
综上，$10$秒后$\triangle PCB$的面积等于$300$平方厘米。

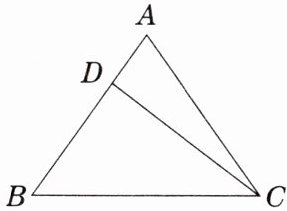
2. 已知等腰$\triangle ABC的底边BC = 20cm$,$D是腰AB$上一点,且$CD = 16cm$,$BD = 12cm$.
(1)求$\triangle ABC$的周长；
(2)求$\triangle ABC$的面积.

答案：
(1) 设 $ AB = AC = x \, cm $，则 $ AD = AB - BD = x - 12 \, cm $。
在 $ \triangle BDC $ 中，$ BD = 12 \, cm $，$ CD = 16 \, cm $，$ BC = 20 \, cm $，
因为 $ 12^2 + 16^2 = 20^2 $，所以 $ \triangle BDC $ 是直角三角形，$ \angle BDC = 90° $，则 $ \angle ADC = 90° $。
在 $ Rt\triangle ADC $ 中，由勾股定理得：$ AD^2 + CD^2 = AC^2 $，
即 $ (x - 12)^2 + 16^2 = x^2 $，解得 $ x = \frac{50}{3} $。
周长为 $ 2 × \frac{50}{3} + 20 = \frac{160}{3} \, cm $。
(2) 过 $ A $ 作 $ AE \perp BC $ 于 $ E $，则 $ BE = EC = 10 \, cm $。
在 $ Rt\triangle AEC $ 中，$ AC = \frac{50}{3} \, cm $，$ EC = 10 \, cm $，
由勾股定理得 $ AE^2 + 10^2 = \left( \frac{50}{3} \right)^2 $，解得 $ AE = \frac{40}{3} \, cm $。
面积为 $ \frac{1}{2} × 20 × \frac{40}{3} = \frac{400}{3} \, cm^2 $。
(1) $ \frac{160}{3} \, cm $；
(2) $ \frac{400}{3} \, cm^2 $。