《2025年学习之友八年级数学上册北师大版》

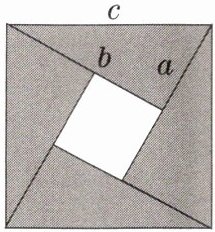
1. 如图是四个全等的直角三角形的拼图,你能验证勾股定理吗？试试看.

答案： 设大正方形的边长为 $c$，四个全等的直角三角形的每条直角边分别为 $a$ 和 $b$。
大正方形的面积为 $c^2$。
四个直角三角形的总面积为 $4 × \frac{1}{2}ab = 2ab$。
中间小正方形的边长为 $b - a$（假设 $b ＞ a$），其面积为 $(b - a)^2$。
根据图形，大正方形的面积等于四个直角三角形的面积加上中间小正方形的面积，即：
$c^2 = 2ab + (b - a)^2$
$c^2 = 2ab + b^2 - 2ab + a^2$
$c^2 = a^2 + b^2$
根据以上推导，验证了勾股定理：$c^2 = a^2 + b^2$。

2. 由四个全等的直角三角形和一个正方形组成的正方形 $ABCD$ 的面积为 $196$,若 $AE = 6$,则正方形 $EFGH$ 的面积是 100.

答案： 100

3. 作八个全等的直角三角形(两条直角边长分别为 $a$,$b$,斜边长为 $c$),再作三个边长分别为 $a$,$b$,$c$ 的正方形,把它们拼成两个正方形(如图),你能利用这两个图形验证勾股定理吗？写出你的验证过程.

答案： 验证过程：
图1分析：
大正方形边长为 $a + b$，面积为 $(a + b)^2$。
该正方形由4个全等直角三角形、1个边长为 $a$ 的正方形和1个边长为 $b$ 的正方形组成。
4个直角三角形面积：$4 × \frac{1}{2}ab = 2ab$。
两个小正方形面积：$a^2 + b^2$。
总面积：$a^2 + b^2 + 2ab$。
图2分析：
大正方形边长为 $a + b$，面积为 $(a + b)^2$。
该正方形由4个全等直角三角形和1个边长为 $c$ 的正方形组成。
4个直角三角形面积：$4 × \frac{1}{2}ab = 2ab$。
边长为 $c$ 的正方形面积：$c^2$。
总面积：$c^2 + 2ab$。
等量关系：
两图中大正方形面积相等，即：
$a^2 + b^2 + 2ab = c^2 + 2ab$。
两边同时减去 $2ab$，得：$a^2 + b^2 = c^2$。
结论：勾股定理得证，即直角三角形两直角边的平方和等于斜边的平方。

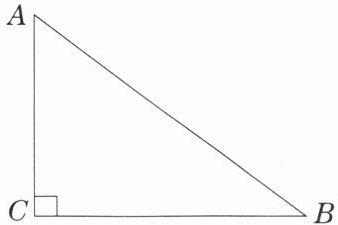
4. 已知直角三角形的两直角边长分别为 $6$ 和 $8$,求它斜边上的高.

答案： 解：设直角三角形为 $Rt\triangle ABC$，$\angle C=90°$，$AC=6$，$BC=8$，斜边 $AB$ 上的高为 $h$。
由勾股定理得：$AB=\sqrt{AC^2+BC^2}=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10$。
$\triangle ABC$ 的面积 $S=\frac{1}{2}AC\cdot BC=\frac{1}{2}×6×8=24$。
又因为 $S=\frac{1}{2}AB\cdot h$，所以 $24=\frac{1}{2}×10× h$，解得 $h=\frac{24×2}{10}=4.8$。
答：斜边上的高为 $4.8$。

1. 求图中阴影部分的面积.
(1)
(2)

答案：
(1) 在Rt△ABC中，∠A=90°，AB=8，AC=6，由勾股定理得BC²=AB²+AC²=8²+6²=100，
∴BC=10，圆的半径r=5。
半圆面积=1/2πr²=1/2π×5²=12.5π，△ABC面积=1/2×AB×AC=1/2×8×6=24。
阴影面积=半圆面积-△ABC面积=12.5π-24。
(2) 阴影部分为梯形，上底BD=3cm，下底AC=5cm，高CB=12cm。
梯形面积=(上底+下底)×高÷2=(3+5)×12÷2=48cm²。
(1)12.5π-24
(2)48cm²

2. 在 $\triangle ABC$ 中,$\angle ACB = 90^{\circ}$,则三个半圆的面积关系是(B).

 
A. $S_{1} + S_{2} ＞ S_{3}$
B. $S_{1} + S_{2} = S_{3}$
C. $S_{1} + S_{2} ＜ S_{3}$
D. $S_{1}^{2} + S_{2}^{2} = S_{3}^{2}$

答案： B

3. 同学们准备召开新年晚会,班长搬来一架高 $2.5$ m 的木梯,准备把拉花挂到 $2.4$ m 高的墙上,则梯脚与墙脚距离应为(A).
A.$0.7$ m
B.$0.8$ m
C.$0.9$ m
D.$1.0$ m

答案： A

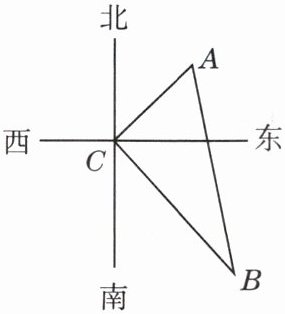
4. 如图,有两艘渔船同时离开某港口去捕鱼,其中一艘以 $16$ 海里 / 时的速度向东南方向航行,另一艘以 $12$ 海里 / 时的速度向东北方向航行,求它们离开港口一个半小时后相距有多远？

答案： 设向东南方向航行的船为$A$，向东北方向航行的船为$B$，港口为$C$，
由题意得：
向东南方向航行的船一个半小时后的行程：$AC = 16 × 1.5 = 24$（海里），
向东北方向航行的船一个半小时后的行程：$BC = 12 × 1.5 = 18$（海里），
因为两船分别向东南和东北方向航行，即方向互相垂直，
所以$\angle ACB=90°$，
在$Rt\triangle ABC$中，由勾股定理得：
$AB=\sqrt{AC^2+BC^2}$
$=\sqrt{24^2+18^2}$
$=\sqrt{576+324}$
$=\sqrt{900}$
$=30$（海里）
综上所述，它们离开港口一个半小时后相距30海里。