第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
7. 某同学家购买了一款加湿器,随着加湿器的运行,房间湿度随之发生变化.设房间湿度为 $ y\% $,其中 $ y $ 与运行时间 $ t $(单位:$ h $)呈现一次函数关系.若加湿器在运行前,房间湿度为 $ 35\% $(房间初始湿度为 $ 35\% $),经过 $ 1 $ 小时 $ 40 $ 分钟后,房间湿度为 $ 40\% $.
(1)求 $ y $ 与 $ t $ 之间的函数关系式.
(2)加湿器一直在运行中,问再经过多长时间,房间湿度达到 $ 55\% $?
(1)求 $ y $ 与 $ t $ 之间的函数关系式.
(2)加湿器一直在运行中,问再经过多长时间,房间湿度达到 $ 55\% $?
答案:
(1)$y=3t+35$
(2)5h
解:
(1)设y与t之间的函数关系式为$y=kt+b$(k、b为常数,且$k≠0$),
1小时40分钟$=(1+\dfrac{40}{60})$小时$=\dfrac{5}{3}$小时,
根据题意得$b=35$,$\dfrac{5}{3}k+b=40$,所以$k=3$,
所以y与t之间的函数关系式为$y=3t+35$.
(2)当$y=55$时,$3t+35=55$,
解得$t=\dfrac{20}{3}$,$\dfrac{20}{3}-\dfrac{5}{3}=5(h)$.
答:再经过5h,房间湿度达到55%.
(1)$y=3t+35$
(2)5h
解:
(1)设y与t之间的函数关系式为$y=kt+b$(k、b为常数,且$k≠0$),
1小时40分钟$=(1+\dfrac{40}{60})$小时$=\dfrac{5}{3}$小时,
根据题意得$b=35$,$\dfrac{5}{3}k+b=40$,所以$k=3$,
所以y与t之间的函数关系式为$y=3t+35$.
(2)当$y=55$时,$3t+35=55$,
解得$t=\dfrac{20}{3}$,$\dfrac{20}{3}-\dfrac{5}{3}=5(h)$.
答:再经过5h,房间湿度达到55%.
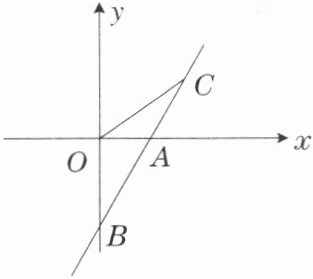
1. 直线 $ AB $ 与 $ x $ 轴交于点 $ A(1,0) $,与 $ y $ 轴交于点 $ B(0,-2) $.
(1)求直线 $ AB $ 的解析式;
(2)若直线 $ AB $ 上的点 $ C $ 在第一象限,且 $ S_{\triangle BOC} = 2 $,求点 $ C $ 的坐标.
(1)求直线 $ AB $ 的解析式;
(2)若直线 $ AB $ 上的点 $ C $ 在第一象限,且 $ S_{\triangle BOC} = 2 $,求点 $ C $ 的坐标.

答案:
解:由题意可知
(1)设$y=kx-2$,将$A(1,0)$代入
$0=k-2$$k=2$
$\therefore y=2x-2$
(2)过点C作$CD\perp y$轴于点D
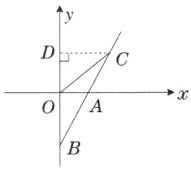
$\because S_{\triangle BOC}=2$
$\therefore \dfrac{1}{2}\cdot OB\cdot CD=2$
$\dfrac{1}{2}× 2\cdot CD=2$,$CD=2$
将$x=2$代入
$y=2x-2=2× 2-2=2$
$\therefore C(2,2)$
解:由题意可知
(1)设$y=kx-2$,将$A(1,0)$代入
$0=k-2$$k=2$
$\therefore y=2x-2$
(2)过点C作$CD\perp y$轴于点D

$\because S_{\triangle BOC}=2$
$\therefore \dfrac{1}{2}\cdot OB\cdot CD=2$
$\dfrac{1}{2}× 2\cdot CD=2$,$CD=2$
将$x=2$代入
$y=2x-2=2× 2-2=2$
$\therefore C(2,2)$
2. 某食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选择.
方案一:从包装盒加工厂直接购买,购买所需的费用 $ y_1 $ 与包装盒数 $ x $ 满足如图 $ 1 $ 所示的函数关系.
方案二:租赁机器自己加工,所需费用 $ y_2 $(包括租赁机器的费用和生产包装盒的费用)与包装盒数 $ x $ 满足如图 $ 2 $ 所示的函数关系.
 根据图象回答下列问题:
根据图象回答下列问题:
(1)方案一中每个包装盒的价格是多少元?
(2)方案二中租赁机器的费用是多少元?生产一个包装盒的费用是多少元?
(3)请分别求出 $ y_1 $、$ y_2 $ 与 $ x $ 的函数关系式.
(4)你认为如果某食品加工厂需要包装盒 $ 6 $ 万个应该选择哪种方案更省钱?并说明理由.
方案一:从包装盒加工厂直接购买,购买所需的费用 $ y_1 $ 与包装盒数 $ x $ 满足如图 $ 1 $ 所示的函数关系.
方案二:租赁机器自己加工,所需费用 $ y_2 $(包括租赁机器的费用和生产包装盒的费用)与包装盒数 $ x $ 满足如图 $ 2 $ 所示的函数关系.
 根据图象回答下列问题:
根据图象回答下列问题:(1)方案一中每个包装盒的价格是多少元?
(2)方案二中租赁机器的费用是多少元?生产一个包装盒的费用是多少元?
(3)请分别求出 $ y_1 $、$ y_2 $ 与 $ x $ 的函数关系式.
(4)你认为如果某食品加工厂需要包装盒 $ 6 $ 万个应该选择哪种方案更省钱?并说明理由.
答案:
解:
(1)如图所示,每个包装盒的价格是
$500÷ 100=5(元/个)$
(2)如图所示,租赁机器的费用是20000元,生产一个包装盒的费用是$(30000-20000)÷ 4000=2.5(元/个)$
(3)$y_{1}=5x$$y_{2}=2.5x+20000$
(4)当$x=60000$时代入
$y_{1}=5× 60000=300000$
$y_{2}=2.5× 60000+20000=170000$
$\because 300000>170000$,
$\therefore$选择方案二.
(1)如图所示,每个包装盒的价格是
$500÷ 100=5(元/个)$
(2)如图所示,租赁机器的费用是20000元,生产一个包装盒的费用是$(30000-20000)÷ 4000=2.5(元/个)$
(3)$y_{1}=5x$$y_{2}=2.5x+20000$
(4)当$x=60000$时代入
$y_{1}=5× 60000=300000$
$y_{2}=2.5× 60000+20000=170000$
$\because 300000>170000$,
$\therefore$选择方案二.
查看更多完整答案,请扫码查看


