《2025年学习之友八年级数学上册北师大版》

1. 估计 20 的算术平方根的大小在(C)。
A.2 和 3 之间
B.3 和 4 之间
C.4 和 5 之间
D.5 和 6 之间

答案： C

2. 对于 1234567,利用计算器不断进行开方运算,随着开方次数的不断增加,其结果(A)。
A.越来越接近 1
B.越来越接近 0
C.没有什么规律
D.越来越大

答案： A

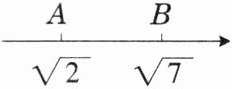
3. 下面数轴上点 A 和点 B 之间的整数是2。
]

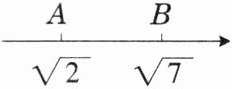
答案： 2

4. 在实数 $ 0,-\sqrt{3},\sqrt{2},-2 $ 中,最小的数是$-2$。

答案： $-2$（题目中是求填具体数，按照要求这里应理解为选对应的表示$-2$的选项，若以常规选项设置，答案选对应$-2$的选项）。

5. 与 $ \sqrt{10}-1 $ 最接近的整数是2。

答案： 2

6. 用估算法比较下列数的大小：
(1) $ -\sqrt{2} $ 与 $ -\sqrt{5} $；
(2) $ 5\sqrt{6} $ 与 $ 6\sqrt{5} $；
(3) $ \sqrt{5} $ 与 2.24；
(4) $ \frac{\sqrt{7}-2}{2} $ 与 $ \frac{1}{2} $。

答案：
(1) 因为$\sqrt{2} ＜ \sqrt{5}$，所以$-\sqrt{2} ＞ -\sqrt{5}$。
(2) $5\sqrt{6} = \sqrt{25×6} = \sqrt{150}$，$6\sqrt{5} = \sqrt{36×5} = \sqrt{180}$，因为$\sqrt{150} ＜ \sqrt{180}$，所以$5\sqrt{6} ＜ 6\sqrt{5}$。
(3) $2.24^2 = 5.0176$，因为$\sqrt{5} \approx 2.236$，$2.236 ＜ 2.24$，所以$\sqrt{5} ＜ 2.24$。
(4) $\sqrt{7} \approx 2.645$，$\sqrt{7} - 2 \approx 0.645$，$\frac{0.645}{2} \approx 0.3225$，因为$0.3225 ＜ 0.5$，所以$\frac{\sqrt{7}-2}{2} ＜ \frac{1}{2}$。

7. 利用计算器,求下列各式的值。(结果精确到 0.001)
(1) $ \sqrt{90} $；
(2) $ \sqrt[3]{\frac{45}{7}} $；
(3) $ \sqrt{0.00123} $；

答案：
(1) 使用计算器计算，$\sqrt{90}\approx9.4868$，精确到$0.001$为$9.487$。
(2) 先计算$\frac{45}{7}\approx6.4286$，再用计算器求立方根，$\sqrt[3]{6.4286}\approx1.853$，精确到$0.001$为$1.853$。
(3) 使用计算器计算，$\sqrt{0.00123}\approx0.03507$，精确到$0.001$为$0.035$。
(1) $9.487$
(2) $1.853$
(3) $0.035$

8. 已知长方形的长与宽的比为 $ 3:2 $,对角线长为 $ \sqrt{39} \mathrm{cm} $,求这个长方形的长和宽。(结果精确到 $ 0.01 \mathrm{cm} $)

答案： 设长方形的长为 $3x \, cm$，宽为 $2x \, cm$。
由勾股定理得：$(3x)^2 + (2x)^2 = (\sqrt{39})^2$
化简得：$9x^2 + 4x^2 = 39$
即：$13x^2 = 39$
解得：$x^2 = 3$，$x = \sqrt{3} \approx 1.732$（负值舍去）
长：$3x \approx 3 × 1.732 = 5.196 \approx 5.20 \, cm$
宽：$2x \approx 2 × 1.732 = 3.464 \approx 3.46 \, cm$
答：长方形的长约为 $5.20 \, cm$，宽约为 $3.46 \, cm$。