《2025年学习之友八年级数学上册北师大版》

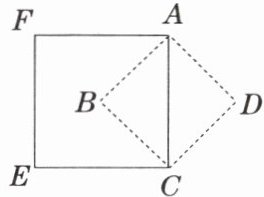
1. 正方形$ABCD的边长为1cm$,以对角线$AC$为边长再作一个正方形,则正方形$ACEF$的面积是2$cm^{2}$.

答案： 2

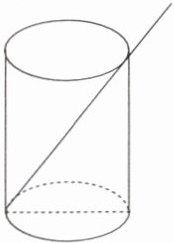
2. 一个透明的圆柱形状的玻璃杯,由内部测得其底面半径为$3cm$,高为$8cm$,今有一支$12cm$的吸管任意斜放于杯中,若不考虑吸管的粗细,吸管露出杯口外的长度最少为2$cm$.

答案： $2$

3. 在一个长$6$米、宽$3$米、高$2$米的房间里放进一根竹竿,则竹竿最长是7米.

答案： 7

4. 小明在广场上先向东走$10$米,又向南走$40$米,再向西走$20$米,又向南走$40$米,再向东走$70$米.求小明到达的终止点与原出发点的距离.

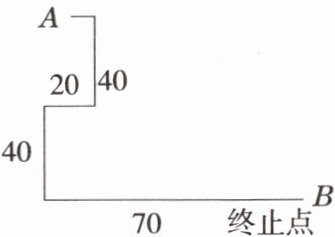
答案： 100米。

5. 已知小龙、阿虎两人均在同一地点,若小龙向北直走$160$米,再向东直走$80$米后,可到百货公司,则阿虎向西直走多少米后,他与百货公司的距离为$340$米？

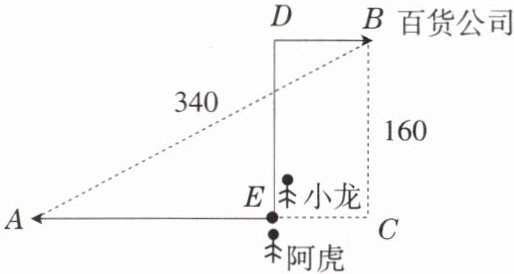
答案： 220米。

6. 为筹备迎新生晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图,已知圆筒高$108cm$,其截面周长为$36cm$,如果在表面恰好缠绕油纸$4$圈,那么应裁剪多长的油纸？

答案： 将圆柱体展开成一个矩形，
这个矩形的宽等于圆柱体截面的周长，即$36cm$，
矩形的长等于圆柱体的高，即$108cm$，
油纸缠绕圆柱体4圈，
因此可以将这个矩形在高度方向上分成4等份，
每份的高度为：
$\frac{108}{4} = 27cm$，
油纸在每一圈的路径可以看作是一个直角三角形的斜边，
直角三角形的两个直角边分别为圆柱体截面的周长（$36cm$）和每一圈的高度（$27cm$），
根据勾股定理，斜边的长度为：
$\sqrt{36^2 + 27^2} = \sqrt{1296 + 729} = \sqrt{2025} = 45cm$，
由于油纸缠绕了4圈，总长度为：
$4 × 45cm = 180cm$。
故应裁剪$180cm$长的油纸。