《2025年学习之友八年级数学上册北师大版》

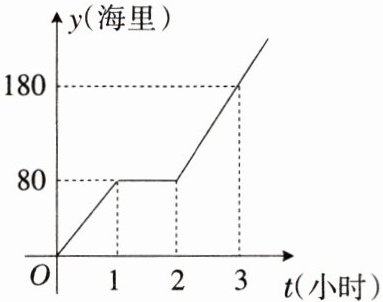
2. 钓鱼岛自古就是中国领土,中国政府已对钓鱼岛开展常态化巡逻.某天,为按计划准点到达相距$480$海里的指定海域,某巡逻艇凌晨$1:00$出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程$y$(海里)与所用时间$t$(小时)的函数图象,则该巡逻艇原计划准点到达的时刻是7:00.

答案： 7:00

3. $A$,$B两地相距1100$米,甲从$A$地出发,乙从$B$地出发,相向而行,甲比乙先出发$2$分钟,乙出发$7$分钟后与甲相遇.设甲、乙两人相距$y$米,甲行进的时间为$t$分钟,$y与t$之间的函数关系如图所示.请你结合图象探究：

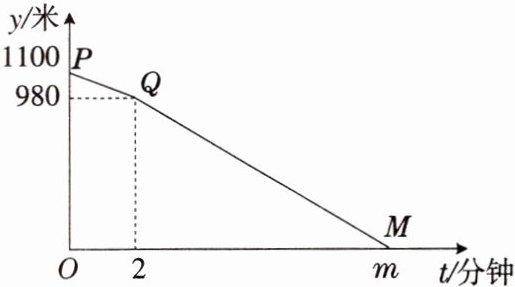
(1) 甲的行进速度为每分钟60米,$m = $9分钟；
(2) 求直线$PQ$对应的函数表达式；
设直线PQ为y = kt + b，将(0,1100)和(2,980)代入得：$\begin{cases}b = 1100 \\ 2k + b = 980\end{cases}$，解得$\begin{cases}k = -60 \\ b = 1100\end{cases}$，所以直线PQ对应的函数表达式为y = -60t + 1100。
(3) 求乙的行进速度.
设乙的行进速度为v₂米/分钟，根据题意得(60 + v₂)×7 = 980，解得v₂ = 80，所以乙的行进速度为80米/分钟。

答案：
(1)Vₐ = (1100 - 980)÷2 = 120÷2 = 60(米/分钟)，m = 2 + 7 = 9(分钟)
(2)设直线PQ为y = 1100 + kt
将(2,980)代入980 = 1100 + 2k
k = -60
∴y = -60t + 1100
(3)(60 + v₂)×7 = 980
v₂ = 80(米/分钟)