第92页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.如图所示,以下几种说法中,正确的个数是(
①$∠3和∠4$是同位角;②$∠6和∠7$是同位角;③$∠4和∠5$是内错角;④$∠2和∠5$是同旁内角;⑤$∠2和∠7$是同位角;⑥$∠1和∠2$是同位角.
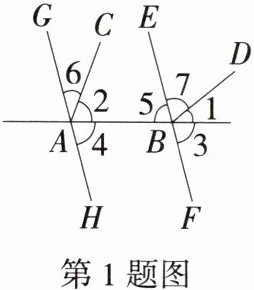
A.3
B.4
C.5
D.6
B
)①$∠3和∠4$是同位角;②$∠6和∠7$是同位角;③$∠4和∠5$是内错角;④$∠2和∠5$是同旁内角;⑤$∠2和∠7$是同位角;⑥$∠1和∠2$是同位角.

A.3
B.4
C.5
D.6
答案:
B 根据同位角、内错角、同旁内角的特征可知,∠3和∠4是同位角;∠1和∠2是同位角;∠4和∠5是内错角;∠2和∠5是同旁内角;∠6和∠7不是同位角;∠2和∠7不是同位角,故正确的为①③④⑥,共4个,故选B.
方法归纳 同位角、内错角、同旁内角的判断方法在判断同位角、内错角、同旁内角时应注意位置特点和图形特点.另外这三类角不管是哪一类,都只涉及三条直线,所以若两个角的两边分别在四条或两条直线上,则都不属于这三类角。
方法归纳 同位角、内错角、同旁内角的判断方法在判断同位角、内错角、同旁内角时应注意位置特点和图形特点.另外这三类角不管是哪一类,都只涉及三条直线,所以若两个角的两边分别在四条或两条直线上,则都不属于这三类角。
2.「2025江苏徐州沛县期中」如图,小明利用两块相同的三角尺,分别在三角尺的边缘画直线AB和CD,并由此判定$AB// CD$,这是根据
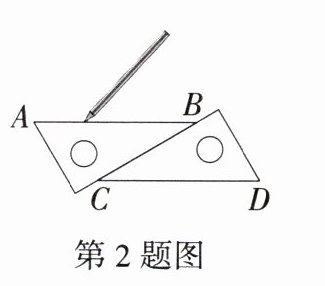
内错角相等
,两直线平行.
答案:
答案 内错角相等
解析 两块相同的三角尺的最小角的位置关系正好是内错角,所以这是根据内错角相等,两直线平行来判定的。
解析 两块相同的三角尺的最小角的位置关系正好是内错角,所以这是根据内错角相等,两直线平行来判定的。
3.如图,$∠BAF= 46^{\circ },∠ACE= 136^{\circ },CE⊥CD$,则$CD// AB$吗? 为什么?
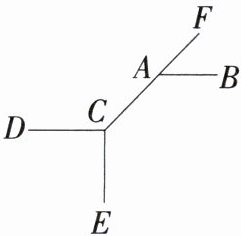

答案:
解析 CD//AB.理由如下:
因为CE⊥CD,所以∠DCE=90°.
因为∠ACE=136°,
所以∠ACD=360°−136°−90°=134°.
因为∠BAF=46°,所以∠BAC=180°−∠BAF=134°,所以∠ACD=∠BAC,所以CD//AB.
因为CE⊥CD,所以∠DCE=90°.
因为∠ACE=136°,
所以∠ACD=360°−136°−90°=134°.
因为∠BAF=46°,所以∠BAC=180°−∠BAF=134°,所以∠ACD=∠BAC,所以CD//AB.
4.如图,在四边形ABCD中,下列推理正确的是(
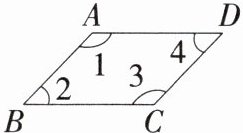
A.因为$∠1+∠2= 180^{\circ }$,所以$AB// CD$
B.因为$∠2+∠3= 180^{\circ }$,所以$AD// BC$
C.因为$∠3+∠4= 180^{\circ }$,所以$AD// BC$
D.因为$∠4+∠2= 180^{\circ }$,所以$AB// CD$
C
)
A.因为$∠1+∠2= 180^{\circ }$,所以$AB// CD$
B.因为$∠2+∠3= 180^{\circ }$,所以$AD// BC$
C.因为$∠3+∠4= 180^{\circ }$,所以$AD// BC$
D.因为$∠4+∠2= 180^{\circ }$,所以$AB// CD$
答案:
C 因为∠1+∠2=180°,所以AD//BC,
故A不符合题意;
因为∠2+∠3=180°,所以AB//CD,
故B不符合题意;
因为∠3+∠4=180°,所以AD//BC,
故C符合题意;
由∠4+∠2=180°,不能判定AB//CD,
故D不符合题意.故选C.
故A不符合题意;
因为∠2+∠3=180°,所以AB//CD,
故B不符合题意;
因为∠3+∠4=180°,所以AD//BC,
故C符合题意;
由∠4+∠2=180°,不能判定AB//CD,
故D不符合题意.故选C.
5.「2024江苏南京秦淮期末,★☆」如图,在$△ABC$中,点D,E,F分别在AC,AB,BC上,以下条件能判定$DE// BC$的是(
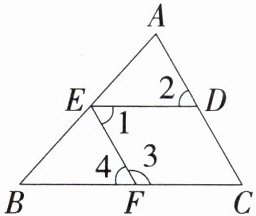
A.$∠1= ∠2$
B.$∠4= ∠C$
C.$∠1+∠3= 180^{\circ }$
D.$∠3+∠C= 180^{\circ }$
C
)
A.$∠1= ∠2$
B.$∠4= ∠C$
C.$∠1+∠3= 180^{\circ }$
D.$∠3+∠C= 180^{\circ }$
答案:
C A.由内错角相等,两直线平行判定EF//AC,不能判定DE//BC,故A不符合题意;B.由同位角相等,两直线平行判定EF//AC,不能判定DE//BC,故B不符合题意;C.由同旁内角互补,两直线平行判定DE//BC,故C符合题意;D.由同旁内角互补,两直线平行判定EF/AC,不能判定DE//BC,故D不符合题意.故选C.
6.新 条件开放题「2024北京大兴期中,★☆」如图,在四边形ABCD中,点F在AD的延长线上,点E在AB的延长线上,如果添加一个条件,使$AB// DC$,那么可添加的条件为
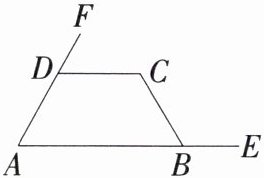
∠FDC=∠A
(写出一个即可).
答案:
答案 ∠FDC=∠A(答案不唯一)
解析 当添加的条件为∠FDC=∠A时,由同位角相等,两直线平行得AB//DC.故答案可以为∠FDC=∠A (答案不唯一).
解析 当添加的条件为∠FDC=∠A时,由同位角相等,两直线平行得AB//DC.故答案可以为∠FDC=∠A (答案不唯一).
7. 分类讨论思想「2025江苏徐州睢宁期中,★☆」如图,直线EF上有两点A、C,分别引两条射线AB、CD,$∠BAF= 110^{\circ }$,CD与AB在直线EF异侧.若$∠DCF= 60^{\circ }$,射线AB、CD分别绕A点、C点以1度/秒和6度/秒的速度同时顺时针转动,设时间为t秒,在射线CD转动一周的时间内,当t的值为____时,CD与AB平行.


答案:
答案 2或38
解析 分三种情况:
如图1,当AB与CD在EF的两侧时,∠ACD=180°−60°−6t°=120°−6t°,∠BAC=110°−t°,
当∠ACD=∠BAF时,AB//CD,
所以120°−6t°=110°−t°,解得t=2,
因为(180°−60°)÷6°=20,
所以0<t<20,所以t=2符合题意.

如图2,当CD旋转到与AB都在EF的右侧时,∠DCF=360°−6t°−60°=300°−6t°,∠BAC=110°−t°,当∠DCF=∠BAC时,AB//CD,
所以300°−6t°=110°−t°,解得t=38,
因为(360°−60°)÷6°=50,
所以20<t<50,所以t=38符合题意.

如图3,当CD旋转到与AB都在EF的左侧时,∠DCF=6t°−(180°−60°+180°)=6t°−300°,∠BAC=t°−110°,当∠DCF=∠BAC时,AB//CD,
所以6t°−300°=t°−110°,解得t=38,
因为此时t>50,但38<50,
所以此种情况不存在.
综上所述,当t的值为2或38时,CD与AB平行.

答案 2或38
解析 分三种情况:
如图1,当AB与CD在EF的两侧时,∠ACD=180°−60°−6t°=120°−6t°,∠BAC=110°−t°,
当∠ACD=∠BAF时,AB//CD,
所以120°−6t°=110°−t°,解得t=2,
因为(180°−60°)÷6°=20,
所以0<t<20,所以t=2符合题意.

如图2,当CD旋转到与AB都在EF的右侧时,∠DCF=360°−6t°−60°=300°−6t°,∠BAC=110°−t°,当∠DCF=∠BAC时,AB//CD,
所以300°−6t°=110°−t°,解得t=38,
因为(360°−60°)÷6°=50,
所以20<t<50,所以t=38符合题意.

如图3,当CD旋转到与AB都在EF的左侧时,∠DCF=6t°−(180°−60°+180°)=6t°−300°,∠BAC=t°−110°,当∠DCF=∠BAC时,AB//CD,
所以6t°−300°=t°−110°,解得t=38,
因为此时t>50,但38<50,
所以此种情况不存在.
综上所述,当t的值为2或38时,CD与AB平行.

查看更多完整答案,请扫码查看


