《2025年5年中考3年模拟七年级数学上册苏科版》

1.下列工具中,有对顶角的是(C)

答案： C　根据对顶角的定义可知，有对顶角的是选项C.方法归纳　识别对顶角的方法
在识别两个角是不是对顶角时，一般先看它们是不是有公共顶点，若没有公共顶点，则它们不是对顶角;若有公共顶点，再看有公共顶点的两个角的两条边是不是都互为反向延长线，若都是，则它们是对顶角;反之，则不是.

2.「2024江苏宿迁宿城期末」泰勒斯被誉为古希腊及西方第一个自然科学家和哲学家,据说“两条直线相交,对顶角相等”就是泰勒斯首次发现并论证的.论证“对顶角相等”使用的依据是(D)
A.等角的补角相等
B.同角的余角相等
C.等角的余角相等
D.同角的补角相等

答案： D　由补角的性质:同角的补角相等，即可判断.

3.「2025江苏镇江丹阳期末」如图,直线AB,CD相交于点O,$∠AOC= 70^{\circ }$,$∠1= 25^{\circ }$,则$∠2= $45$^{\circ }$.

答案： 答案　45
解析　因为∠AOC=70°,∠AOC=∠BOD,所以∠BOD=70°.因为∠1=25°,所以∠2=∠BOD−∠1=70°−25°=45°.

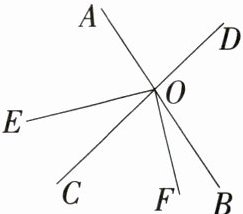
4.「2024江苏淮安洪泽月考」如图所示,直线AB,CD相交于点O,$∠EOF= 90^{\circ }$,$∠AOD= 80^{\circ }$,且$∠FOC= 2∠EOC$,求$∠EOB$的度数.

答案： 解析　因为∠EOF=90°,∠FOC=2∠EOC,所以∠EOC= $\frac{1}{3}$×90°=30°.因为∠AOD=80°,所以∠BOC=∠AOD=80°,所以∠EOB=∠EOC+∠BOC=30°+80°=110°.

5.「2024江苏南京建邺月考,★☆」如图,直线AB,CD相交于点O,OE平分$∠BOD$,OF平分$∠COE$.若$∠AOC的度数为2\alpha $,则$∠EOF= $$90^{\circ}-\frac{\alpha}{2}$.(用含$\alpha $的代数式表示)

答案： 答案　$90^{\circ}-\frac{\alpha}{2}$
解析　因为∠AOC=2α,所以∠BOD=∠AOC=2α.因为OE平分∠BOD,OF平分∠COE,所以∠BOE=∠DOE=α,∠COF=∠EOF= $\frac{1}{2}$∠COE.因为∠COE+∠DOE=180°,所以∠COE=180°-α,所以∠EOF= $90^{\circ}-\frac{\alpha}{2}$.

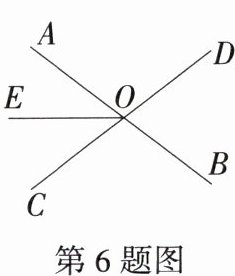
6.学科分类讨特色论思想「2025上海徐汇华育中学月考,★☆」如图,直线AB,CD相交于点O,已知$∠BOD= 75^{\circ }$,OE把$∠AOC$分成两个角,且$∠AOE= ∠EOC$,将射线OE绕点O逆时针旋转$\alpha (0^{\circ }＜\alpha ＜360^{\circ })$到OF,当$∠AOF= 120^{\circ }$时,$\alpha $的度数是______.

答案：
答案　82.5°或202.5°
解析　①当OF在∠BOC内部时,如图1,因为∠BOD=75°,所以∠AOC=∠BOD=75°,所以∠AOE=∠EOC=37.5°,因为∠AOF=120°,所以∠COF=∠AOF−∠AOC=45°,所以∠EOF=∠EOC+∠COF=82.5°,所以α=82.5°;
　　　
②当OF在∠BOD内部时,如图2,因为∠AOF=120°,∠AOE=37.5°,所以∠EOF=∠AOF+∠AOE=157.5°,所以α=360°−∠EOF=202.5°.
故答案为82.5°或202.5°.

7.「2025江苏徐州沛县月考,★☆」如图,直线AB,CD交于点O,OE平分$∠AOD$,OF平分$∠BOD$.
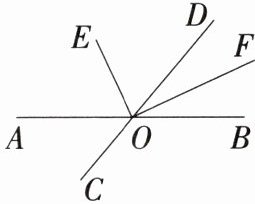
(1)若$∠AOC= 50^{\circ }$,求$∠DOF与∠DOE$的度数,并计算$∠EOF$的度数.
(2)当$∠AOC$的度数变化时,$∠EOF$的度数是否变化？若不变,求其值；若变化,说明理由.

答案： 解析　
(1)因为∠AOC=50°,所以∠BOD=∠AOC=50°,因为OF平分∠BOD,所以∠DOF= $\frac{1}{2}$∠BOD= $\frac{1}{2}$×50°=25°,因为∠AOC+∠AOD=180°,所以∠AOD=180°-∠AOC=180°-50°=130°,因为OE平分∠AOD,所以∠DOE= $\frac{1}{2}$∠AOD= $\frac{1}{2}$×130°=65°,所以∠EOF=∠DOF+∠DOE=25°+65°=90°.
(2)当∠AOC的度数变化时,∠EOF的度数没有变化.理由:因为OF平分∠BOD,所以∠DOF= $\frac{1}{2}$∠BOD.因为OE平分∠AOD,所以∠DOE= $\frac{1}{2}$∠AOD,所以∠EOF=∠DOF+∠DOE= $\frac{1}{2}$∠BOD+ $\frac{1}{2}$∠AOD= $\frac{1}{2}$(∠AOD+∠BOD)= $\frac{1}{2}$∠AOB=90°.