第88页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.下列说法中,正确的个数为 ( )
①两条直线相交所成的四个角中,如果有两个角相等,那么这两条直线垂直;
②两条直线相交所成的四个角中,如果有一个角是直角,那么这两条直线垂直;
③一条直线的垂线可以画无数条;
④在同一平面内,经过一个已知点能画一条且只能画一条直线与已知直线垂直.
A.1
B.2
C.3
D.4
①两条直线相交所成的四个角中,如果有两个角相等,那么这两条直线垂直;
②两条直线相交所成的四个角中,如果有一个角是直角,那么这两条直线垂直;
③一条直线的垂线可以画无数条;
④在同一平面内,经过一个已知点能画一条且只能画一条直线与已知直线垂直.
A.1
B.2
C.3
D.4
答案:
C 如图,直线a和b相交所成的四个角中,∠1=∠2,∠3=∠4,但a与b不垂直,故①说法不正确;②③④说法均正确。故选C。

C 如图,直线a和b相交所成的四个角中,∠1=∠2,∠3=∠4,但a与b不垂直,故①说法不正确;②③④说法均正确。故选C。

2.「2024北京中考」如图,直线AB和CD相交于点O,$OE⊥OC$.若$∠AOC= 58^{\circ }$,则$∠EOB$的大小为 (
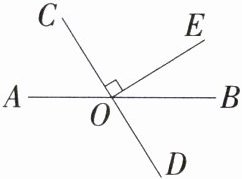
A.$29^{\circ }$
B.$32^{\circ }$
C.$45^{\circ }$
D.$58^{\circ }$
B
)
A.$29^{\circ }$
B.$32^{\circ }$
C.$45^{\circ }$
D.$58^{\circ }$
答案:
B 因为OE⊥OC,所以∠COE=90°。
因为∠AOC+∠COE+∠EOB=180°,∠AOC=58°,
所以∠EOB=180°−90°−58°=32°。故选B。
因为∠AOC+∠COE+∠EOB=180°,∠AOC=58°,
所以∠EOB=180°−90°−58°=32°。故选B。
3.(1)如图1,过点P画AB的垂线.
(2)如图2,过点P分别画OA,OB的垂线.
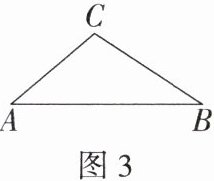
(3)如图3,过点A画BC的垂线.
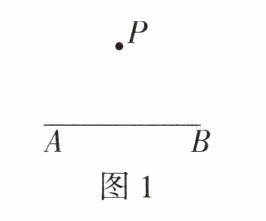
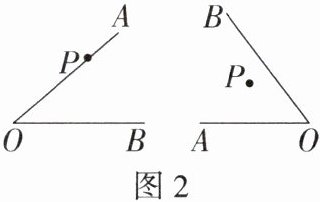
(2)如图2,过点P分别画OA,OB的垂线.
(3)如图3,过点A画BC的垂线.



答案:
解析
(1)如图1所示。
(2)如图2所示。
(3)如图3所示。



方法归纳 画垂线一般用直角三角尺来画,通常情况下要标出垂足。在画某线段的垂线时,如果垂线与它无交点,那么需要延长该线段,再作垂线,得到垂线与直线的交点,进而标出垂足。
解析
(1)如图1所示。
(2)如图2所示。
(3)如图3所示。



方法归纳 画垂线一般用直角三角尺来画,通常情况下要标出垂足。在画某线段的垂线时,如果垂线与它无交点,那么需要延长该线段,再作垂线,得到垂线与直线的交点,进而标出垂足。
4.「2024江苏宿迁期末」若$AB⊥a,AC⊥a$,则A,B,C三点共线,理由是
在同一平面内,过一点有且只有一条直线与已知直线垂直
.
答案:
答案 在同一平面内,过一点有且只有一条直线与已知直线垂直
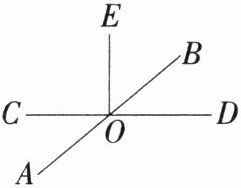
5.「2025浙江宁波镇海期末,」如图,直线AB,CD相交于点O,$EO⊥CD$于点O.若$∠BOD:∠BOC= 2:7$,则$∠AOE$的度数为______.

130°
答案:
答案 130°
解析 因为∠BOD:∠BOC=2:7,∠BOD+∠BOC=180°,所以∠BOD=2/9×180°=40°,
所以∠AOC=∠BOD=40°,
因为EO⊥CD,所以∠EOC=90°,
所以∠AOE=∠EOC+∠AOC=90°+40°=130°。
解析 因为∠BOD:∠BOC=2:7,∠BOD+∠BOC=180°,所以∠BOD=2/9×180°=40°,
所以∠AOC=∠BOD=40°,
因为EO⊥CD,所以∠EOC=90°,
所以∠AOE=∠EOC+∠AOC=90°+40°=130°。
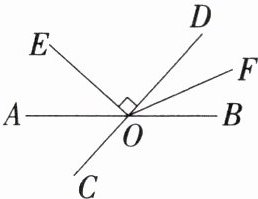
6.学科方程特色思想「2024江苏南京玄武期末,」如图,直线AB,CD相交于点O,$OE⊥CD$,OF平分$∠BOD$,若$∠AOE+∠BOF= 66^{\circ }$,则$∠BOC=$______$^{\circ }$.

132
答案:
答案 132
解析 设∠AOE=α,∠BOF=β。
因为∠AOE+∠BOF=66°,
所以α+β=66°,所以β=66°−α。
因为OF平分∠BOD,
所以∠DOF=∠BOF=β,
所以∠DOB=∠DOF+∠BOF=2β。
因为OE⊥CD,所以∠EOD=90°。
因为∠AOE+∠EOD+∠DOB=180°,
所以α+90°+2β=180°,所以α+2β=90°,
所以α+2(66°−α)=90°,解得α=42°,即∠AOE=42°,所以∠AOD=∠AOE+∠EOD=42°+90°=132°,
所以∠BOC=∠AOD=132°。
解析 设∠AOE=α,∠BOF=β。
因为∠AOE+∠BOF=66°,
所以α+β=66°,所以β=66°−α。
因为OF平分∠BOD,
所以∠DOF=∠BOF=β,
所以∠DOB=∠DOF+∠BOF=2β。
因为OE⊥CD,所以∠EOD=90°。
因为∠AOE+∠EOD+∠DOB=180°,
所以α+90°+2β=180°,所以α+2β=90°,
所以α+2(66°−α)=90°,解得α=42°,即∠AOE=42°,所以∠AOD=∠AOE+∠EOD=42°+90°=132°,
所以∠BOC=∠AOD=132°。
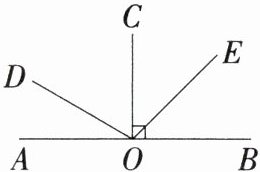
7.「2025江苏盐城东台期末,」如图,已知$OC⊥AB$于O,$∠AOD:∠COD= 1:2$.
(1)若OE平分$∠BOC$,求$∠DOE$的度数.
(2)若$∠AOE的度数比∠COE$的度数的3倍多$30^{\circ }$,试判断OD与OE的位置关系,并说明理由.
(1)若OE平分$∠BOC$,求$∠DOE$的度数.
(2)若$∠AOE的度数比∠COE$的度数的3倍多$30^{\circ }$,试判断OD与OE的位置关系,并说明理由.

答案:
解析
(1)因为OC⊥AB,
所以∠AOC=∠BOC=90°。
因为∠AOD:∠COD=1:2,
所以∠DOC=2/3∠AOC=60°,
因为OE平分∠BOC,
所以∠COE=1/2∠BOC=45°,
所以∠DOE=∠DOC+∠COE=60°+45°=105°。
(2)OD⊥OE。理由如下:
由
(1)知∠AOC=∠BOC=90°,∠DOC=60°,
由题意得∠AOE=3∠COE+30°,
即∠AOE−∠COE=2∠COE+30°,
因为∠AOE=∠AOC+∠COE,
所以∠AOE−∠COE=∠AOC=90°,
所以2∠COE+30°=90°,所以∠COE=30°,
所以∠DOE=∠DOC+∠COE=60°+30°=90°,
所以OD⊥OE。
(1)因为OC⊥AB,
所以∠AOC=∠BOC=90°。
因为∠AOD:∠COD=1:2,
所以∠DOC=2/3∠AOC=60°,
因为OE平分∠BOC,
所以∠COE=1/2∠BOC=45°,
所以∠DOE=∠DOC+∠COE=60°+45°=105°。
(2)OD⊥OE。理由如下:
由
(1)知∠AOC=∠BOC=90°,∠DOC=60°,
由题意得∠AOE=3∠COE+30°,
即∠AOE−∠COE=2∠COE+30°,
因为∠AOE=∠AOC+∠COE,
所以∠AOE−∠COE=∠AOC=90°,
所以2∠COE+30°=90°,所以∠COE=30°,
所以∠DOE=∠DOC+∠COE=60°+30°=90°,
所以OD⊥OE。
查看更多完整答案,请扫码查看


