第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
9.[2025江苏南师附中树人学校月考]一个半径为3 cm,高为5 cm的圆柱,将它的侧面沿虚线剪开(如图),剪开后得到一个平行四边形,这个平行四边形的面积是
30π
cm².
答案:
答案 30π
解析 圆柱的侧面积为2×3π×5=30π(cm²),所以这个平行四边形的面积是30π cm²。
解析 圆柱的侧面积为2×3π×5=30π(cm²),所以这个平行四边形的面积是30π cm²。
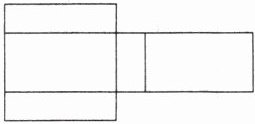
10.[2025江苏泰州兴化期末]小明在学习了“展开与折叠”这一课后,掌握了长方体盒子的制作方法.如图所示的是他制作的一个半成品的平面图.
(1)在图中补充一个长方形,使该平面图能折叠成一个长方体盒子.
(2)已知小明制作的长方体盒子的长是宽的2倍,宽是高的2倍,且长方体所有棱长的和为56 cm,求这个长方体盒子的体积.
(1)在图中补充一个长方形,使该平面图能折叠成一个长方体盒子.
(2)已知小明制作的长方体盒子的长是宽的2倍,宽是高的2倍,且长方体所有棱长的和为56 cm,求这个长方体盒子的体积.

答案:
解析
(1)如图所示(答案不唯一):

(2)设长方体盒子的高为a cm,则宽为2a cm,长为4a cm,根据题意,得4(a+2a+4a)=56,解得a=2。所以这个长方体盒子的高为2 cm,宽为4 cm,长为8 cm,所以这个长方体盒子的体积为2×4×8=64(cm³)。
解析
(1)如图所示(答案不唯一):

(2)设长方体盒子的高为a cm,则宽为2a cm,长为4a cm,根据题意,得4(a+2a+4a)=56,解得a=2。所以这个长方体盒子的高为2 cm,宽为4 cm,长为8 cm,所以这个长方体盒子的体积为2×4×8=64(cm³)。
11.新 空间观念[2025江苏无锡新吴期末]【问题情境】
“制作无盖的长方体纸盒”是苏科版七年级上册的课题学习,某综合实践小组在学习了这一课后,开展了“长方体纸盒的制作”实践活动.
【问题解决】
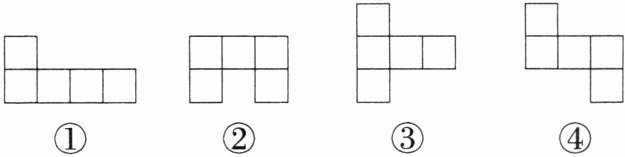
(1)在如图所示的图形中,是无盖正方体的表面展开图的是____.(填序号)
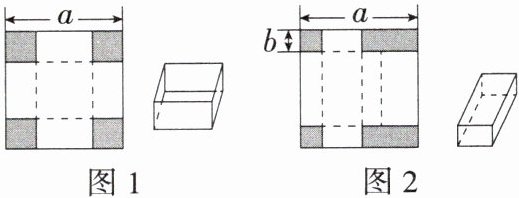
(2)综合实践小组利用边长为a cm的正方形纸板制作出两种不同方案的长方体纸盒(图1为无盖的长方体纸盒,图2为有盖的长方体纸盒).
(i)按图1所示的方式制作一个无盖的长方体纸盒的方法:先在纸板四角剪去四个同样大小的边长为x cm的小正方形,再沿虚线折合起来,则长方体纸盒的底面周长为____cm.
(ii)按图2所示的方式制作一个有盖的长方体纸盒的方法:先在纸板四角剪去两个同样大小的边长为b cm的小正方形和两个同样大小的小长方形,再沿虚线折合起来.如果a= 30,b= 5,则该长方体纸盒的体积为$____cm^3.$
【问题进阶】
(3)若一个无盖长方体的长、宽、高分别为6、4、3,它缺一个长为6,宽为4的长方形底面,将它的表面沿某些棱剪开,展开成一个平面图形,则该长方体表面展开图的最大外围周长为____;通过比较长方体表面展开图取得最大外围周长和最小外围周长的两个图形,你发现了什么规律?你发现的规律是____.
“制作无盖的长方体纸盒”是苏科版七年级上册的课题学习,某综合实践小组在学习了这一课后,开展了“长方体纸盒的制作”实践活动.
【问题解决】
(1)在如图所示的图形中,是无盖正方体的表面展开图的是____.(填序号)

(2)综合实践小组利用边长为a cm的正方形纸板制作出两种不同方案的长方体纸盒(图1为无盖的长方体纸盒,图2为有盖的长方体纸盒).
(i)按图1所示的方式制作一个无盖的长方体纸盒的方法:先在纸板四角剪去四个同样大小的边长为x cm的小正方形,再沿虚线折合起来,则长方体纸盒的底面周长为____cm.
(ii)按图2所示的方式制作一个有盖的长方体纸盒的方法:先在纸板四角剪去两个同样大小的边长为b cm的小正方形和两个同样大小的小长方形,再沿虚线折合起来.如果a= 30,b= 5,则该长方体纸盒的体积为$____cm^3.$
【问题进阶】
(3)若一个无盖长方体的长、宽、高分别为6、4、3,它缺一个长为6,宽为4的长方形底面,将它的表面沿某些棱剪开,展开成一个平面图形,则该长方体表面展开图的最大外围周长为____;通过比较长方体表面展开图取得最大外围周长和最小外围周长的两个图形,你发现了什么规律?你发现的规律是____.

答案:
解析
(1)①③④。
(2)(i)题图1所折成的长方体纸盒的底面是边长为(a - 2x)cm的正方形,因此长方体纸盒的底面周长为4×(a - 2x)=(4a - 8x)cm。故答案为(4a - 8x)。
(ii)由题意可知,所折成的长方体纸盒的长为a - 2b = 20 cm,宽为$\frac{a - 2b}{2}$ = 10 cm,高为5 cm,所以体积为20×10×5 = 1000(cm³)。故答案为1000。
(3)要使长方体表面展开图的外围周长最大,则剪开的棱越长越好,即没有剪开的棱越短越好,如图所示,其展开图的外围周长最大。

所以最大外围周长为58 cm。
发现规律:没有剪开的棱越短,展开图的外围周长越大。
解析
(1)①③④。
(2)(i)题图1所折成的长方体纸盒的底面是边长为(a - 2x)cm的正方形,因此长方体纸盒的底面周长为4×(a - 2x)=(4a - 8x)cm。故答案为(4a - 8x)。
(ii)由题意可知,所折成的长方体纸盒的长为a - 2b = 20 cm,宽为$\frac{a - 2b}{2}$ = 10 cm,高为5 cm,所以体积为20×10×5 = 1000(cm³)。故答案为1000。
(3)要使长方体表面展开图的外围周长最大,则剪开的棱越长越好,即没有剪开的棱越短越好,如图所示,其展开图的外围周长最大。

所以最大外围周长为58 cm。
发现规律:没有剪开的棱越短,展开图的外围周长越大。
查看更多完整答案,请扫码查看


