第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.观察下面“品”字形中各数之间的规律,根据观察到的规律得出a的值为(
A.75
B.128
C.139
D.141
D
)A.75
B.128
C.139
D.141
答案:
D
2.将一列有理数-1,2,-3,4,-5,6,…按如图所示的方式有序排列.根据图中的排列规律可知“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰6”中C的位置是有理数
-29
,-1027应排在A、B、C、D、E中的A
的位置.
答案:
-29;A
3.观察下面的一列数:$\frac {1}{2},-\frac {2}{3},\frac {1}{4},-\frac {4}{5},\frac {1}{6},-\frac {6}{7},...$,请你找出排列的规律,解答下列问题:
(1)第9个数是
(2)如果这一组数无限排列下去,与哪两个数越来越接近?
(1)第9个数是
$\frac{1}{10}$
,第14个数是$-\frac{14}{15}$
,第99个数是$\frac{1}{100}$
,第2025个数是$\frac{1}{2026}$
.(2)如果这一组数无限排列下去,与哪两个数越来越接近?
如果这一组数无限排列下去,与0和-1越来越接近.
答案:
(1)$\frac{1}{10}$;$-\frac{14}{15}$;$\frac{1}{100}$;$\frac{1}{2026}$
(2)如果这一组数无限排列下去,与0和-1越来越接近.
(1)$\frac{1}{10}$;$-\frac{14}{15}$;$\frac{1}{100}$;$\frac{1}{2026}$
(2)如果这一组数无限排列下去,与0和-1越来越接近.
4.观察下列单项式的特点:
$\frac {1}{2}x^{2}y,-\frac {1}{4}x^{2}y^{2},\frac {1}{8}x^{2}y^{3},-\frac {1}{16}x^{2}y^{4},...$
(1)写出第8个单项式.
(2)猜想第n个单项式是什么,并指出它的系数和次数.
$\frac {1}{2}x^{2}y,-\frac {1}{4}x^{2}y^{2},\frac {1}{8}x^{2}y^{3},-\frac {1}{16}x^{2}y^{4},...$
(1)写出第8个单项式.
(2)猜想第n个单项式是什么,并指出它的系数和次数.
答案:
(1)第8个单项式为$-\frac{1}{2^8}x^2y^8$
(2)第n个单项式是$(-1)^{n+1}×(\frac{1}{2})^n x^2y^n$,它的系数是$(-1)^{n+1}×(\frac{1}{2})^n$,次数为n+2.
(1)第8个单项式为$-\frac{1}{2^8}x^2y^8$
(2)第n个单项式是$(-1)^{n+1}×(\frac{1}{2})^n x^2y^n$,它的系数是$(-1)^{n+1}×(\frac{1}{2})^n$,次数为n+2.
5.「2024山东济宁中考」如图,用大小相等的小正方形按照一定规律拼正方形.第一幅图中有1个正方形,第二幅图中有5个正方形,第三幅图中有14个正方形,……,按照此规律,第六幅图中正方形的个数为(
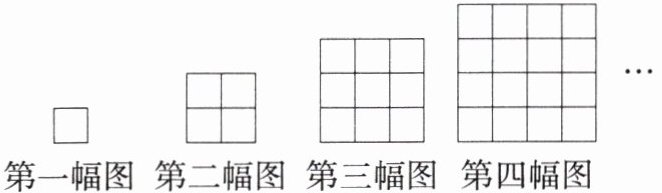
A.90
B.91
C.92
D.93
B
)
A.90
B.91
C.92
D.93
答案:
B
6.【观察思考】
下图是由正方形和等边三角形组成的一系列图案,其中第1个图案有4个正方形;第2个图案有6个正方形;第3个图案有8个正方形;……
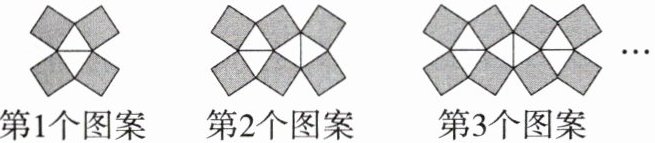
依此规律,请解答下面的问题.
【规律发现】
(1)第5个图案有
(2)第n个图案有
【规律应用】
(3)结合图案中正方形的排列方式,现有4050个正方形,若干个等边三角形(足够多).依此规律,是否可以组成第n个图案(正方形一次性用完)?若可以,请求出n的值;若不可以,请说明理由.
下图是由正方形和等边三角形组成的一系列图案,其中第1个图案有4个正方形;第2个图案有6个正方形;第3个图案有8个正方形;……

依此规律,请解答下面的问题.
【规律发现】
(1)第5个图案有
12
个正方形.(2)第n个图案有
(2n+2)
个正方形.【规律应用】
(3)结合图案中正方形的排列方式,现有4050个正方形,若干个等边三角形(足够多).依此规律,是否可以组成第n个图案(正方形一次性用完)?若可以,请求出n的值;若不可以,请说明理由.
可以,n=2024
答案:
(1)12
(2)(2n+2)
(3)可以,n=2024
(1)12
(2)(2n+2)
(3)可以,n=2024
查看更多完整答案,请扫码查看


