第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
9. 多解法「2025江苏无锡新吴月考,」小明在计算$2-4+6-8+10-12+14-16$时,不小心把7个运算符号中的一个写错了(“+”错写成“-”或“-”错写成“+”),结果算成了16,则原式从左往右数,运算符号写错的是(
A.第6个
B.第5个
C.第4个
D.第3个
B
)A.第6个
B.第5个
C.第4个
D.第3个
答案:
B 【解法一】第1个符号写错时,2+4+6-8+10-12+14-16=0;第2个符号写错时,2-4-6-8+10-12+14-16=-20;第3个符号写错时,2-4+6+8+10-12+14-16=8;第4个符号写错时,2-4+6-8-10-12+14-16=-28;第5个符号写错时,2-4+6-8+10+12+14-16=16;第6个符号写错时,2-4+6-8+10-12-14-16=-36;第7个符号写错时,2-4+6-8+10-12+14+16=24.则原式从左往右数,运算符号写错的是第5个.故选B.
【解法二】正确计算2-4+6-8+10-12+14-16=-8,因为写错一个运算符号后结果为16,16-(-8)=24,24÷2=12,所以运算错误的是-12,错算成+12,故运算符号写错的是第5个.
【解法二】正确计算2-4+6-8+10-12+14-16=-8,因为写错一个运算符号后结果为16,16-(-8)=24,24÷2=12,所以运算错误的是-12,错算成+12,故运算符号写错的是第5个.
10. 「2025江苏扬州高邮月考,」计算:$-8+(-\frac{3}{8})+\vert -3\vert -(-\frac{1}{8})-0.75= $
-6
.
答案:
-6
解析 原式$=-8-\frac{3}{8}+3+\frac{1}{8}-\frac{3}{4}=(-8+3)+(-\frac{3}{8}+\frac{1}{8}-\frac{3}{4})=-5+(-1)=-6.$
解析 原式$=-8-\frac{3}{8}+3+\frac{1}{8}-\frac{3}{4}=(-8+3)+(-\frac{3}{8}+\frac{1}{8}-\frac{3}{4})=-5+(-1)=-6.$
11. 「2024江苏泰州泰兴实验初中月考,」计算:$(-5\frac{1}{2})-(-3\frac{1}{4})+(+2\frac{3}{4})-(+\frac{1}{2})$.
小敏的做法如下:
解:原式$=(-5\frac{1}{2})+3\frac{1}{4}+2\frac{3}{4}-\frac{1}{2}$(第一步)
$=[(-5\frac{1}{2})-\frac{1}{2}]+(3\frac{1}{4}+2\frac{3}{4})$(第二步)
$=-5+6$(第三步)
$=1$.(第四步)
根据小敏的计算过程,回答下列问题:
(1)小敏在进行第二步计算时,运用了加法的
(2)请指出她从第
(3)请你写出正确的解题过程.
小敏的做法如下:
解:原式$=(-5\frac{1}{2})+3\frac{1}{4}+2\frac{3}{4}-\frac{1}{2}$(第一步)
$=[(-5\frac{1}{2})-\frac{1}{2}]+(3\frac{1}{4}+2\frac{3}{4})$(第二步)
$=-5+6$(第三步)
$=1$.(第四步)
根据小敏的计算过程,回答下列问题:
(1)小敏在进行第二步计算时,运用了加法的
交换
律、结合
律.(2)请指出她从第
三
步开始出现错误.(3)请你写出正确的解题过程.
原式$=(-5\frac{1}{2})+3\frac{1}{4}+2\frac{3}{4}-\frac{1}{2}=(-5\frac{1}{2})-\frac{1}{2}+(3\frac{1}{4}+2\frac{3}{4})=-6+6=0.$
答案:
(1)交换;结合.
(2)三.
(3)原式$=(-5\frac{1}{2})+3\frac{1}{4}+2\frac{3}{4}-\frac{1}{2}=(-5\frac{1}{2})-\frac{1}{2}+(3\frac{1}{4}+2\frac{3}{4})=-6+6=0.$
(1)交换;结合.
(2)三.
(3)原式$=(-5\frac{1}{2})+3\frac{1}{4}+2\frac{3}{4}-\frac{1}{2}=(-5\frac{1}{2})-\frac{1}{2}+(3\frac{1}{4}+2\frac{3}{4})=-6+6=0.$
12. 「2025江苏徐州睢宁中学联考,」七年级(4)班的几位同学正在一起讨论一个关于数轴上的点表示数的题目.
甲说:“这条数轴上的两个点A、B表示的数都是绝对值是5的数,且A在B的左边.”
乙说:“点C表示正整数,点D表示负整数,且这两个数的差是2.”
丙说:“点E表示的数的相反数是它本身.”
(1)请你根据以上三位同学的发言,画出一条数轴,并描出A、B、C、D、E五个不同的点.
(2)求这五个点表示的数的和.
甲说:“这条数轴上的两个点A、B表示的数都是绝对值是5的数,且A在B的左边.”
乙说:“点C表示正整数,点D表示负整数,且这两个数的差是2.”
丙说:“点E表示的数的相反数是它本身.”
(1)请你根据以上三位同学的发言,画出一条数轴,并描出A、B、C、D、E五个不同的点.
(2)求这五个点表示的数的和.
答案:
(1)由题意可知点A表示的数为-5,点B表示的数为5.因为点C表示正整数,点D表示负整数,且这两个数的差是2,所以点C表示的数为1,点D表示的数为-1.因为点E表示的数的相反数是它本身,所以点E表示的数为0.画出数轴及描点如下: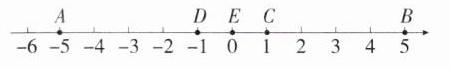
(2)-5+5+1+(-1)+0=0.
(1)由题意可知点A表示的数为-5,点B表示的数为5.因为点C表示正整数,点D表示负整数,且这两个数的差是2,所以点C表示的数为1,点D表示的数为-1.因为点E表示的数的相反数是它本身,所以点E表示的数为0.画出数轴及描点如下:
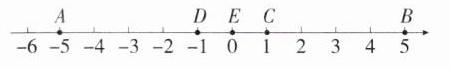
(2)-5+5+1+(-1)+0=0.
13. 推理能力「2024江苏无锡期中」桌子上有7张反面向上的纸牌,每次翻转n张(n为正整数)纸牌,多次操作后能使所有纸牌正面向上吗?用“+1”“-1”分别表示一张纸牌“正面向上”“反面向上”,将所有纸牌的对应值相加得到总和,我们的目标是将总和从-7变化为+7.
(1)当$n= 1$时,每翻转1张纸牌,总和的变化量是2或-2,则最少
(2)当$n= 2$时,每翻转2张纸牌,总和的变化量是
(3)若要使多次操作后所有纸牌全部正面向上,写出n的所有可能的值.
(1)当$n= 1$时,每翻转1张纸牌,总和的变化量是2或-2,则最少
7
次操作后所有纸牌全部正面向上.(2)当$n= 2$时,每翻转2张纸牌,总和的变化量是
4,-4,0
,多次操作后能使所有纸牌全部正面向上吗?若能,最少需要几次操作?若不能,简要说明理由.不能,理由:要使所有纸牌正面向上,总变化量为14,而14无法由4,-4,0相加得到.
(3)若要使多次操作后所有纸牌全部正面向上,写出n的所有可能的值.
1,3,5,7
答案:
(1)7
(2)4,-4,0;不能,理由:要使所有纸牌正面向上,总变化量为14,而14无法由4,-4,0相加得到.
(3)1,3,5,7
(1)7
(2)4,-4,0;不能,理由:要使所有纸牌正面向上,总变化量为14,而14无法由4,-4,0相加得到.
(3)1,3,5,7
查看更多完整答案,请扫码查看


