《2025年5年中考3年模拟七年级数学上册苏科版》

13. 下列关于代数式$4x+2y$的意义叙述正确的有①②.(填序号)
①x的4倍与y的2倍的和是$4x+2y$；
②小明以x米/分钟的速度跑了4分钟,再以y米/分钟的速度跑了2分钟,小明一共跑了$(4x+2y)$米；
③苹果的价格为每千克x元,橘子的价格为每千克y元,买4千克橘子、2千克苹果一共花费$(4x+2y)$元.

答案： ①②

14. 「2025江苏南京玄武期中」已知代数式$x^2-2y+1$的值是-2,则代数式$2-2x^2+4y$的值是8.

答案： 8

15. 「2025江苏苏州昆山期中改编」若$2m-1,4-m$这两个有理数在数轴上所对应的点分别A,B,且点A在点B的左侧,则A,B两点之间的距离可以表示为$5-3m$.

答案： $5-3m$

16. 新考向 「2025江苏无锡江阴期中」已知a是不为1的有理数,我们把$\frac{1}{1-a}$称为a的差倒数,如：2的差倒数是$\frac{1}{1-2}= -1$, -1的差倒数是$\frac{1}{1-(-1)}= \frac{1}{2}$.已知$a_1= -\frac{1}{3}$,$a_2是a_1$的差倒数,$a_3是a_2$的差倒数,$a_4是a_3$的差倒数,……,以此类推,则$a_{2024}= $$\frac{3}{4}$.

答案： $\frac{3}{4}$

17. 「2025江苏镇江期中」(6分)在数轴上把下列各数表示出来,并用“＜”连接各数.
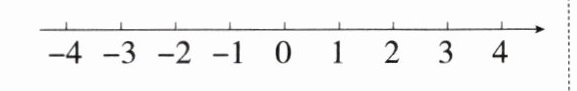
$-|-1|,0,+(-3.5),(-2)^2$.

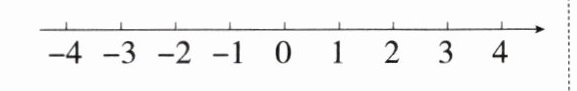
答案： $-|-1|=-1$,$+(-3.5)=-3.5$,$(-2)^2=4$,将各数在数轴上表示如图所示. $+(-3.5)＜-|-1|＜0＜(-2)^2$

18. 「2025江苏南通通州期中」(16分)计算：
(1)$-\frac{1}{4}-(+3\frac{1}{2})+2.25-(-\frac{1}{2})$.
(2)$(1\frac{3}{8}+2\frac{1}{3}-3.75)×24$.
(3)$-1^4-\frac{2}{3}×(-12)-(11-5^2)$.
(4)$(3x^2y-7xy^2)-2(4xy^2-\frac{3}{2}x^2y)$.

答案：
(1)原式$=-\frac{1}{4}+2.25-3\frac{1}{2}+\frac{1}{2}=2-3=-1$.
(2)原式$=\frac{11}{8}×24+\frac{7}{3}×24-\frac{15}{4}×24=33+56-90=-1$.
(3)原式$=-1-(-8)-(11-25)=-1+8-(-14)=-1+8+14=21$.
(4)原式$=3x^2y-7xy^2-8xy^2+3x^2y=3x^2y+3x^2y-7xy^2-8xy^2=6x^2y-15xy^2$

19. 「2025江苏常州金坛期中」(6分)化简并求值：
$3(2a^2b-4ab^2)-(-3a^2b+6ab^2)$,其中$a= 1,b= -\frac{1}{3}$.

答案： $3(2a^2b-4ab^2)-(-3a^2b+6ab^2)=6a^2b-12ab^2+3a^2b-6ab^2=9a^2b-18ab^2$.当$a=1$,$b=-\frac{1}{3}$时,原式$=9×1^2×(-\frac{1}{3})-18×1×(-\frac{1}{3})^2=-9×1×\frac{1}{3}-18×1×\frac{1}{9}=-3-2=-5$

20. (8分)已知$A= 3x^2+5xy-7y-3,B= x^2-xy+2$.
(1)求$3A-(2A+3B)$的值.
(2)若$A-3B$的值与y的取值无关,求x的值.

答案：
(1)$3A-(2A+3B)=3A-2A-3B=A-3B$.因为$A=3x^2+5xy-7y-3$,$B=x^2-xy+2$,所以$A-3B=(3x^2+5xy-7y-3)-3(x^2-xy+2)=3x^2+5xy-7y-3-3x^2+3xy-6=8xy-7y-9$.
(2)$A-3B=8xy-7y-9=(8x-7)y-9$,因为$A-3B$的值与y的取值无关,所以$8x-7=0$,所以$x=\frac{7}{8}$