《2025年5年中考3年模拟七年级数学上册苏科版》

1. 如图,已知线段 $ AB = 12 \text{ cm} $,点 $ C $ 为线段 $ AB $ 上的一个动点,点 $ D $,$ E $ 分别是 $ AC $,$ BC $ 的中点。

(1) 若 $ AC = 4 \text{ cm} $,求 $ DE $ 的长。
因为AB=12cm,AC=4cm,所以BC=AB−AC=8cm.因为点D,E分别是AC,BC的中点,所以DC=$\frac{1}{2}$AC=2cm,CE=$\frac{1}{2}$BC=4cm,所以DE=DC+CE=6cm.
(2) 若 $ C $ 为 $ AB $ 的中点,则 $ AD $ 与 $ AB $ 的数量关系是______。
AD=$\frac{1}{4}$AB(或AB=4AD)
(3) 试着说明,无论点 $ C $ 在线段 $ AB $ 上如何运动,只要不与点 $ A $,$ B $ 重合,那么 $ DE $ 的长不变。
因为点D是AC的中点,所以DC=$\frac{1}{2}$AC,因为点E是BC的中点,所以CE=$\frac{1}{2}$CB,所以DE=DC+CE=$\frac{1}{2}$AC+$\frac{1}{2}$CB=$\frac{1}{2}$AB=6cm,所以无论点C在线段AB上如何运动,只要不与点A,B重合,那么DE的长不变.

答案：
(1)因为AB=12cm,AC=4cm,所以BC=AB−AC=8cm.因为点D,E分别是AC,BC的中点,所以DC=$\frac{1}{2}$AC=2cm,CE=$\frac{1}{2}$BC=4cm,所以DE=DC+CE=6cm.
(2)因为C为AB的中点,所以AC=$\frac{1}{2}$AB,因为点D是AC的中点,所以AD=$\frac{1}{2}$AC=$\frac{1}{2}$×$\frac{1}{2}$AB=$\frac{1}{4}$AB.故答案为AD=$\frac{1}{4}$AB(或AB=4AD).
(3)因为点D是AC的中点,所以DC=$\frac{1}{2}$AC,因为点E是BC的中点,所以CE=$\frac{1}{2}$CB,所以DE=DC+CE=$\frac{1}{2}$AC+$\frac{1}{2}$CB=$\frac{1}{2}$AB=6cm,所以无论点C在线段AB上如何运动,只要不与点A,B重合,那么DE的长不变.

2. 如图,$ C $ 是线段 $ AB $ 上一点,$ AB = 20 \text{ cm} $,$ BC = 8 \text{ cm} $,点 $ P $ 从点 $ A $ 出发,以 $ 2 \text{ cm/s} $ 的速度沿 $ AB $ 向右运动,终点为 $ B $；点 $ Q $ 从点 $ B $ 出发,以 $ 1 \text{ cm/s} $ 的速度沿 $ BA $ 向左运动,终点为 $ A $。已知 $ P $,$ Q $ 同时出发,当其中一点到达终点时,另一点也随之停止运动。设点 $ P $ 的运动时间为 $ t $ 秒。

(1) 当 $ P $,$ Q $ 两点重合时,求 $ t $ 的值。
(2) 是否存在某一时刻,使得 $ C $,$ P $,$ Q $ 这三个点中,有一个点恰好是另外两点所连线段的中点？若存在,求出所有满足条件的 $ t $ 值；若不存在,请说明理由。

答案：
(1)由题意得AP=2tcm,BQ=tcm,当P,Q两点重合时,AP+BQ=20cm,即2t+t=20,解得t=$\frac{20}{3}$.
(2)存在.因为AB=20cm,BC=8cm,所以AC=AB−BC=20−8=12(cm),当点C是线段PQ的中点时,PC=QC,即12−2t=8−t,解得t=4.当点P是线段CQ的中点时,CP=QP,即2t−12=20−3t,解得t=$\frac{32}{5}$.当点Q是线段PC的中点时,PQ=CQ,即t−(20−2t)=8−t,解得t=7.综上所述,t的值为4或$\frac{32}{5}$或7.

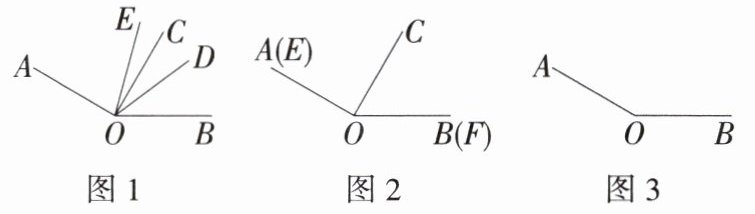
3. 已知 $ \angle AOB = 150^{\circ} $,$ OC $ 为 $ \angle AOB $ 内部的一条射线,$ \angle BOC = 60^{\circ} $。
(1) 如图 1,若 $ OE $ 平分 $ \angle AOB $,$ OD $ 为 $ \angle BOC $ 内部的一条射线,$ \angle COD = \frac{1}{2} \angle BOD $,求 $ \angle DOE $ 的度数。
(2) 如图 2,若射线 $ OE $ 绕着 $ O $ 点从 $ OA $ 开始以 15 度/秒的速度顺时针旋转至 $ OB $ 结束,$ OF $ 绕着 $ O $ 点从 $ OB $ 开始以 5 度/秒的速度逆时针旋转至 $ OA $ 结束,设运动时间为 $ t $ 秒,当 $ \angle EOC = \angle FOC $ 时,求 $ t $ 的值。
(3) 若射线 $ OM $ 绕着 $ O $ 点从 $ OA $ 开始以 15 度/秒的速度逆时针旋转至 $ OB $ 结束,在旋转过程中,$ ON $ 平分 $ \angle AOM $,试问 $ 2 \angle BON - \angle BOM $ 在某时间段内是不是定值？若不是,请说明理由；若是,请在图 3 中补全图形,求出这个定值并写出 $ t $ 所在的时间段。(本题中的角均为大于 $ 0^{\circ} $ 且小于 $ 180^{\circ} $ 的角)

答案：

(1)因为∠AOB=150°,OE平分∠AOB,所以∠EOB=$\frac{1}{2}$∠AOB=75°.因为∠BOC=60°,∠COD=$\frac{1}{2}$∠BOD,所以∠BOD=40°,所以∠DOE=∠EOB−∠BOD=75°−40°=35°.
(2)①当0≤t≤10时,∠EOC=|90°-15°t|,∠FOC=|60°-5°t|,因为∠EOC=∠FOC,所以|90°-15°t|=|60°-5°t|,解得t=3或t=7.5.
②当10＜t≤30时,OE停止运动,此时∠EOC=60°,∠FOC=|60°-5°t|,因为∠EOC=∠FOC,所以60°=|60°-5°t|,解得t=0(舍去)或t=24.综上所述,当∠EOC=∠FOC时,t=3或7.5或24.
(3)①如图1,当0≤t≤2时,∠AOM=15°t,所以∠BOM=150°+15°t,因为ON平分∠AOM,所以∠AON=∠MON=7.5°t,所以∠BON=150°+7.5°t,所以2∠BON−∠BOM=2(150°+7.5°t)−(150°+15°t)=150°,是定值.
　　　
②如图2,当2＜t＜4时,∠AOM=15°t,所以∠BOM=360°−150°−15°t=210°−15°t,因为ON平分∠AOM,所以∠AON=7.5°t,所以∠BON=150°+7.5°t,所以2∠BON−∠BOM=2(150°+7.5°t)−(210°−15°t)=90°+30°t,不是定值.
　　　
③如图3,当4≤t≤12时,∠AOM=15°t,所以∠BOM=210°−15°t,因为ON平分∠AOM,所以∠MON=7.5°t,所以∠BON=210°−15°t+7.5°t=210°−7.5°t,所以2∠BON−∠BOM=2(210°−7.5°t)−(210°−15°t)=210°,是定值.
　　　
④如图4,当12＜t≤14时,∠BOM=210°−15°t,∠MON=$\frac{1}{2}$(360°−15°t)=180°−7.5°t,所以∠BON=180°−7.5°t−(210°−15°t)=7.5°t−30°,所以2∠BON−∠BOM=2(7.5°t−30°)−(210°−15°t)=30°t−270°,不是定值.
综上所述,当0≤t≤2时,2∠BON−∠BOM是定值,定值为150°;当4≤t≤12时,2∠BON−∠BOM是定值,定值为210°.