《2025年5年中考3年模拟七年级数学上册苏科版》

13. (12分)(1)化简：$ a^{2} - 3ab + 10 - 5a^{2} - ab - 7 $。
(2)化简：$ 3a + 2(a - 3b) - (2b - 2a) $。
(3)先化简,再求值：$ 5(2a^{2}b + ab^{2}) - 2(3ab^{2} - a^{2}b) $,其中 $ a = -4,b = \frac{3}{2} $。

答案：
(1)原式$=-4a^{2}-4ab+3.$
(2)原式$=3a+2a-6b-2b+2a=7a-8b.$
(3)原式$=10a^{2}b+5ab^{2}-6ab^{2}+2a^{2}b=12a^{2}b-ab^{2}.$当$a=-4,b=\frac {3}{2}$时,原式$=12×(-4)^{2}×\frac {3}{2}-(-4)×$$(\frac {3}{2})^{2}=288+9=297.$

14. (8分)已知一个两位数,它的十位上的数字是 $ a $,个位上的数字是 $ b(a ＞ b ＞ 0) $。
(1)用含 $ a,b $ 的代数式表示这个两位数。
(2)若把这个两位数的十位上的数字与个位上的数字对换,得到一个新的两位数,则原两位数与新两位数的差能被 9 整除吗？为什么？

答案：
(1)根据题意可得这个两位数为$10a+b.$
(2)原两位数与新两位数的差能被9整除.理由:把这个两位数的十位上的数字与个位上的数字对换,得到的新两位数为$10b+a$,所以原两位数与新两位数的差为$10a+b-(10b+a)=9a-9b=9(a-b),$因为$a＞b＞0$,且 a,b 为整数,所以$9(a-b)$能被9整除,所以原两位数与新两位数的差能被9整除.

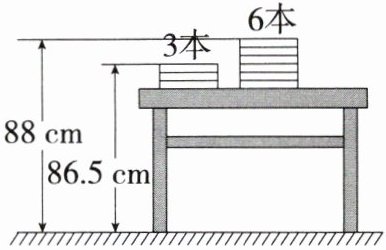
15. [2025 江苏盐城盐都期中](10分)如图,两摞规格完全相同的课本整齐叠放在讲台上。请根据图中所给出的数据信息,回答下列问题：
(1)每本课本的厚度为______cm。
(2)若有一摞上述规格的课本 $ x $ 本,整齐叠放在讲台上,请用含 $ x $ 的代数式表示出这一摞课本的顶部距离地面的高度。
(3)当 $ x = 55 $ 时,若从中取走 13 本,求余下的课本的顶部距离地面的高度。

(1)0.5
(2)(0.5x+85)cm
(3)106 cm

答案：
(1)根据题意,得三本课本的高度为 88-86.5=1.5(cm),故每本课本的厚度为$1.5÷3=0.5(cm),$故答案为0.5.
(2)因为三本课本的高度为$88-86.5=1.5(cm),$所以桌面距离地面的高度为$86.5-1.5=85(cm),$因为每本课本的厚度为0.5 cm,所以x本课本的高度为0.5x cm,所以这一摞课本的顶部距离地面的高度为$(0.5x+85)cm.$
(3)根据题意,得x本课本顶部距离地面的高度为$(0.5x+85)cm$,当$x=55-13=42$时,$0.5x+85=0.5×$$42+85=106$.故余下的课本的顶部距离地面的高度为106 cm.

16. [2025 江苏扬州江都期中](10分)某校餐厅计划购买一批餐桌和餐椅。现从甲、乙两商场了解到：同一型号的餐桌报价为每张 200 元,餐椅报价为每把 50 元。某商店开展促销活动,可以向顾客提供两种优惠方案：
方案一：每购买一张餐桌赠送一把餐椅；
方案二：所有餐桌、餐椅均按报价的 90%付款。
现某班级要购买餐桌 20 张,餐椅 $ x $ 把($ x $ 大于 20)。
(1)若该班级按方案一购买,需付款(50x+3000)元；若该班级按方案二购买,需付款(45x+3600)元。(用含 $ x $ 的式子表示)
(2)当 $ x = 30 $ 时,哪种方案更划算？请通过计算说明理由。
方案一更划算.理由如下:当x=30时,方案一的费用为50x+3000=50×30+3000=4500(元),方案二的费用为45x+3600=45×30+3600=4950(元),因为4500＜4950,所以方案一更划算.
(3)若两种方案可以同时使用,当 $ x = 40 $ 时,你能给出一种最省钱的购买方案吗？试写出你的购买方案,并计算该方案所需的付款金额。
方案:用方案一购买20张桌子和20张椅子,再用方案二购买20张椅子,所需的付款金额为20×200+20×50×0.9=4000+900=4900(元).

答案：
(1)方案一:200×20+50(x-20)=(50x+3000)元；方案二:0.9(200×20+50x)=(45x+3600)元.故答案为(50x+3000);(45x+3600).
(2)方案一更划算.理由如下:当x=30时,方案一的费用为50x+3000=50×30+3000=4500(元),方案二的费用为45x+3600=45×30+3600=4950(元),因为4500＜4950,所以方案一更划算.
(3)方案:用方案一购买20张桌子和20张椅子,再用方案二购买20张椅子,所需的付款金额为20×200+20×50×0.9=4000+900=4900(元).