第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
9.「」有理数$a$,$b$,$c$在数轴上对应的点的位置如图所示,则$\frac{|a|}{a}+\frac{b}{|b|}+\frac{|c|}{c} = $
-1
.
答案:
-1 解析 由数轴可知a>0,b<0,c<0,所以|a|=a,|b|=-b,|c|=-c,所以$\frac{|a|}{a}$=$\frac{a}{a}$=1,$\frac{b}{|b|}$=$\frac{b}{-b}$=-1,$\frac{|c|}{c}$=$\frac{-c}{c}$=-1,所以$\frac{|a|}{a}$+$\frac{b}{|b|}$+$\frac{|c|}{c}$=-1.
10.「2025 江苏南通崇川月考,」若被除数是$-\frac{7}{2}$,除数比被除数小$\frac{3}{2}$,则商是
$\frac{7}{10}$
.
答案:
$\frac{7}{10}$ 解析 除数是-$\frac{7}{2}$-$\frac{3}{2}$=-5,则商是-$\frac{7}{2}$÷(-5)=$\frac{7}{2}$÷5=$\frac{7}{2}$×$\frac{1}{5}$=$\frac{7}{10}$.
11.「2025 江苏连云港灌南月考,」已知两个数的积是$-\frac{2}{9}$,其中一个数的倒数是$\frac{3}{4}$,则另一个数是
-$\frac{1}{6}$
.
答案:
-$\frac{1}{6}$ 解析 由题意得其中一个数为$\frac{4}{3}$,所以另一个数=-$\frac{2}{9}$÷$\frac{4}{3}$=-$\frac{2}{9}$×$\frac{3}{4}$=-$\frac{1}{6}$.
12.「2025 江苏南京鼓楼求真中学月考,」从$-5$、$-3$、$-1$、2、4 中任取 2 个数,所得积的最大值记为$a$,所得商的最小值记为$b$,则$\frac{a}{b}$的值为
-$\frac{15}{4}$
.
答案:
-$\frac{15}{4}$ 解析 由题意得积的最大值a=-5×(-3)=15,商的最小值b=$\frac{4}{-1}$=-4,所以$\frac{a}{b}$=$\frac{15}{-4}$=-$\frac{15}{4}$.
13.「2025 江苏泰州姜堰月考,」计算: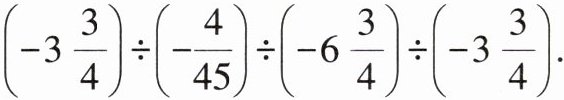
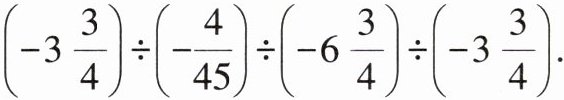
答案:
解析 原式=(-$\frac{15}{4}$)×(-$\frac{45}{4}$)×(-$\frac{4}{27}$)×(-$\frac{4}{15}$)=$\frac{5}{3}$.
14.「2025 江苏无锡锡山月考,」可可在计算$-3 + ■$时,由于不小心,后面的加数被墨水污染了.
(1) 可可问了同桌乐乐,发现乐乐计算时误将$-3$后面的“$+$”看成了“$÷$”,从而算得结果为$-2$,请求出被墨水污染的这个数.
(2) 请你正确计算此题.
(1) 可可问了同桌乐乐,发现乐乐计算时误将$-3$后面的“$+$”看成了“$÷$”,从而算得结果为$-2$,请求出被墨水污染的这个数.
(2) 请你正确计算此题.
答案:
解析
(1)由题可知被墨水污染的数是-3÷(-2)=$\frac{3}{2}$.
(2)-3+$\frac{3}{2}$=-$\frac{3}{2}$.
(1)由题可知被墨水污染的数是-3÷(-2)=$\frac{3}{2}$.
(2)-3+$\frac{3}{2}$=-$\frac{3}{2}$.
15. 如图,数$a$,$b在数轴上的对应点为A$,$B$,记$\frac{a + b}{2}在数轴上的对应点为C$.
| 点 A 表示的数 | 点 B 表示的数 | 点 C 表示的数 |
| $-7$ | $3$ | $\frac{-7 + 3}{2} = -2$ |
| $-9$ | $2$ | $m$ |
| $n$ | $1.5$ | $-3$ |
(1) $m$的值为
(2) 猜想:点$A$,$C间的距离为AC$的长,点$C$,$B间的距离为CB$的长,则$AC$
(3) 在纸条上有一数轴,折叠纸条,若表示$-1$的点与表示 3 的点重合,则表示 2024 的点与表示哪个数的点重合?并说明理由.
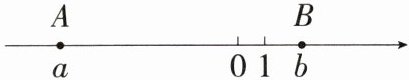
| 点 A 表示的数 | 点 B 表示的数 | 点 C 表示的数 |
| $-7$ | $3$ | $\frac{-7 + 3}{2} = -2$ |
| $-9$ | $2$ | $m$ |
| $n$ | $1.5$ | $-3$ |
(1) $m$的值为
-3.5
,$n$的值为-7.5
.(2) 猜想:点$A$,$C间的距离为AC$的长,点$C$,$B间的距离为CB$的长,则$AC$
=
$CB$.(用“$<$”“$>$”或“$=$”填空)(3) 在纸条上有一数轴,折叠纸条,若表示$-1$的点与表示 3 的点重合,则表示 2024 的点与表示哪个数的点重合?并说明理由.
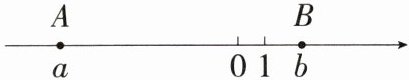
表示2024的点与表示-2022的点重合.理由:因为表示-1的点与表示3的点重合,$\frac{-1+3}{2}$=1,$\frac{-2022+2024}{2}$=1,所以表示2024的点与表示-2022的点重合.
答案:
解析
(1)$\frac{-9+2}{2}$=-3.5,-3×2-1.5=-7.5,故答案为-3.5;-7.5.
(2)=.
(3)表示2024的点与表示-2022的点重合.理由:因为表示-1的点与表示3的点重合,$\frac{-1+3}{2}$=1,$\frac{-2022+2024}{2}$=1,所以表示2024的点与表示-2022的点重合.
(1)$\frac{-9+2}{2}$=-3.5,-3×2-1.5=-7.5,故答案为-3.5;-7.5.
(2)=.
(3)表示2024的点与表示-2022的点重合.理由:因为表示-1的点与表示3的点重合,$\frac{-1+3}{2}$=1,$\frac{-2022+2024}{2}$=1,所以表示2024的点与表示-2022的点重合.
16. 观察下列等式:(式子中的“$!$”是一种数学运算符号)
$1! = 1$,
$2! = 2×1$,
$3! = 3×2×1$,
$4! = 4×3×2×1$,
……
请计算$\frac{2024!}{2023!}$的值.
$1! = 1$,
$2! = 2×1$,
$3! = 3×2×1$,
$4! = 4×3×2×1$,
……
请计算$\frac{2024!}{2023!}$的值.
答案:
解析 原式=$\frac{2024×2023×2022×…×2×1}{2023×2022×…×2×1}$=2024.
查看更多完整答案,请扫码查看


