《2025年5年中考3年模拟七年级数学上册苏科版》

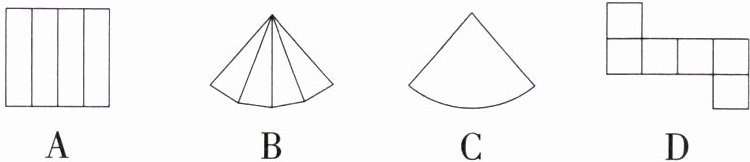
1.「2024江苏常州中考」下列图形中,为四棱锥的侧面展开图的是 (B)

答案： B 四棱锥的侧面展开图是四个三角形.故选B.

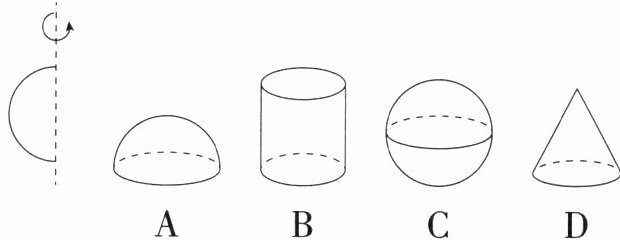
2.「2024陕西中考」如图,将半圆绕直径所在的虚线旋转一周,得到的立体图形是 (C)

答案： C 将半圆绕直径所在的虚线旋转一周,得到的立体图形是球.故选C.

3.「2024江苏扬州中考」如图所示的是将某几何体的表面展开后得到的平面图形,则该几何体是 (C)
A.三棱锥
B.圆锥
C.三棱柱
D.长方体

答案： C 由几何体的表面展开后得到的平面图形可知侧面为三个相同的长方形,上、下底面为完全一样的三角形,符合三棱柱的特征,所以该几何体是三棱柱.

4.「2024山东济宁中考」如图所示的是一个正方体的表面展开图,把展开图折叠成正方体后,与“建”字所在面相对的面上的字是 (D)
A.人
B.才
C.强
D.国

答案： D 与“建”字所在面相对的面上的字是“国”.故选D.

5.如图,对于该组图的变换顺序描述正确的是 (B)
A.翻折、旋转、平移
B.翻折、平移、旋转
C.平移、翻折、旋转
D.旋转、翻折、平移

答案： B 由题图可知,变换的顺序依次为翻折、平移、旋转.故选B.

6.下列说法正确的是 (C)
A.棱柱的侧面可以是三角形
B.由六个大小相同的正方形组成的图形是正方体的表面展开图
C.正方体的各条棱长都相等
D.棱柱的各条棱长都相等

答案： C 棱柱的侧面都是平行四边形,故选项A错误；由六个大小相同的正方形组成的图形不一定是正方体的表面展开图,故选项B错误；选项C正确；棱柱的所有侧棱的长都相等,所以选项D错误.

7.「2025江苏连云港灌南月考」用一个平面去截一个几何体,得到的截面是六边形,这个几何体可能是 (D)
A.三棱锥
B.三棱柱
C.四棱锥
D.正方体

答案： D 用一个平面去截一个几何体,得到的截面是六边形,说明该几何体至少有六个面.故选D.

8.七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,如图1所示.19世纪传到国外,被称为“唐图”(意为“来自中国的拼图”),图2是由边长为4的正方形分割制作的七巧板拼摆而成的“叶问蹬”图,则图中抬起的“腿”(阴影部分)的面积为 (A)
A.3
B.$\frac{7}{2}$
C.2
D.$\frac{5}{2}$

答案： A 由题意得,阴影部分中平行四边形的面积=2×1=2,阴影部分中三角形的面积=$\frac{1}{2}$×2×1=1,所以阴影部分的面积=2+1=3.故选A.

9.「2025江苏宿迁宿豫期末」一个几何体的表面能够展开成如图所示的平面图形,则这个几何体的名称是圆柱.

答案： 圆柱

10.「2025江苏泰州姜堰期末」国扇文化有深厚的文化底蕴,历来中国有“制扇王国”之称,打开折扇时,随着扇骨的移动形成一个扇面,这种现象可以用数学原理解释为线动成面.

答案： 线动成面 解析 由题意知,这种现象可以用数学原理解释为线动成面.