《2025年5年中考3年模拟七年级数学上册苏科版》

1.「2024甘肃中考」若$∠A= 55^{\circ }$,则$∠A$的补角为(D)
A.$35^{\circ }$
B.$45^{\circ }$
C.$115^{\circ }$
D.$125^{\circ }$

答案： D　若∠A=55°,则∠A的补角为180°−55°=125°.故选D.

2.学科教材变式学科方程特色$P_{166}$例2特色思想「2024江苏南京玄武期末」一个角的补角比它的余角的2倍多$30^{\circ }$,这个角的度数为30°.

答案： 答案　30° 解析　设这个角的度数为x,由题意得180°−x=2(90°−x)+30°,解得x=30°. 故这个角的度数为30°.

3.「2025江苏镇江丹阳月考」若$∠1与∠2$互余,$∠1与∠3$互补,则$∠3-∠2= $90$^{\circ }$.

答案： 答案　90 解析　因为∠1与∠2互余, 所以∠1+∠2=90°, 所以∠2=90°−∠1. 因为∠1与∠3互补, 所以∠1+∠3=180°, 所以∠3=180°−∠1, 所以∠3−∠2=(180°−∠1)−(90°−∠1)=180°−∠1−90°+∠1=90°.

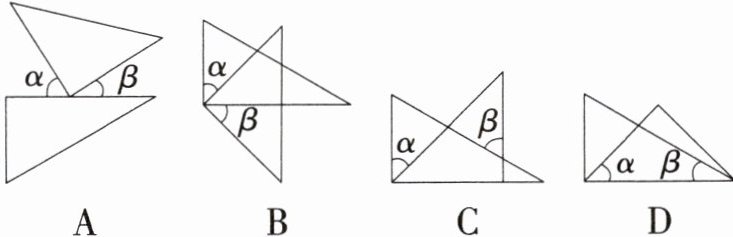
4.「2024浙江杭州期末」将一副三角尺按下列选项中的位置摆放,其中$∠α与∠β$一定相等的是( )

答案：
B　如图,因为∠α、∠β都是∠1的余角， 所以∠α=∠β. 故选B.

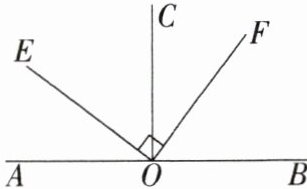
5.如图所示,点O在直线AB上,且$∠AOC= ∠BOC= ∠EOF= 90^{\circ }$,试判断$∠AOE与∠BOF的关系以及∠COE与∠BOF$的关系.

答案： 解析　由题意得,∠AOE+∠BOF=180°−∠EOF=90°,所以∠AOE与∠BOF互余,根据同角的余角相等可得∠COE=∠BOF.

6.「2025江苏苏州期末,★☆」如果$∠α和∠β$互补,且$∠α＞∠β$,那么下列表示$∠β$的余角的式子:①$90^{\circ }-∠β$;②$∠α-90^{\circ }$;③$180^{\circ }-∠α$;④$\frac {1}{2}(∠α-∠β)$,其中正确的是(B)
A.①②③④
B.①②④
C.①②③
D.①②

答案： B　因为∠α与∠β互补,所以∠α+∠β=180°. ∠β的余角=90°−∠β, 所以①正确. 因为∠β=180°−∠α, 所以∠β的余角=90°−∠β=90°−(180°−∠α)=∠α−90°, 所以②正确. 因为∠α+∠β=180°, 所以$\frac{1}{2}$(∠α+∠β)=90°, 所以∠β的余角=90°−∠β=$\frac{1}{2}$(∠α+∠β)−∠β=$\frac{1}{2}$(∠α−∠β), 所以④正确. 因为180°−∠α=∠β, 所以③错误. 故选B.

7.「2025广西南宁月考,★☆」如图,$∠AOB= ∠COD= ∠EOF= 90^{\circ }$,则$∠1,∠2,∠3$之间的数量关系为(D)
A.$∠1+∠2+∠3= 90^{\circ }$
B.$∠1+∠2-∠3= 90^{\circ }$
C.$∠2+∠3-∠1= 90^{\circ }$
D.$∠3-∠2+∠1= 90^{\circ }$

答案： D　因为∠AOB=∠COD=∠EOF=90°, 所以∠DOE=90°−∠1,∠BOC=90°−∠3, 所以∠DOE+∠BOC=180°−∠1−∠3. 因为∠DOE+∠BOC=90°−∠2, 所以180°−∠1−∠3=90°−∠2, 所以∠3−∠2+∠1=90°. 故选D.

8.「2025北京东城期末改编,★☆」如图,点O在直线AB上,$∠BOC= 90^{\circ }$.若$∠DOE= 50^{\circ },∠AOD:∠AOE= 2:3$,则$∠COE$的补角的度数为120°.

答案： 120° 解析　因为∠DOE=50°,∠AOD:∠AOE=2:3, 所以∠AOE=$\frac{3}{5}$∠DOE=30°, 因为∠BOC=90°, 所以∠COE=180°−∠BOC−∠AOE=60°, 所以∠COE的补角的度数=180°−∠COE=120°.

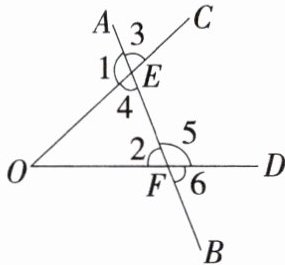
9.「2024江苏南京月考,★☆」如图,直线AB与$∠COD$的两边OC,OD分别相交于点E,F,$∠1+∠2= 180^{\circ }$,找出图中与$∠2$相等的角.

答案： 解析　因为∠1+∠4=180°,∠1+∠3=180°,∠1+∠2=180°, 所以∠4=∠2,∠3=∠2, 因为∠6+∠5=180°,∠2+∠5=180°, 所以∠6=∠2. 综上所述,题图中与∠2相等的角有∠3,∠4,∠6.