第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.下列说法中,正确的个数是 (
①线段AB和线段BA是同一条线段;
②射线AB与射线BA是同一条射线;
③直线AB与直线BA是同一条直线;
④射线AB的长是5cm.
A.1
B.2
C.3
D.4
B
)①线段AB和线段BA是同一条线段;
②射线AB与射线BA是同一条射线;
③直线AB与直线BA是同一条直线;
④射线AB的长是5cm.
A.1
B.2
C.3
D.4
答案:
B 对于①,根据线段的定义可知,线段AB和线段BA 是同一条线段,故①正确;
对于②,射线AB的端点是A,射线BA的端点是B,所以射线AB和射线BA不是同一条射线,故②错误;对于③,根据直线的表示方法可知,直线AB和直线BA是同一条直线,故③正确;
对于④,由射线的定义可知,射线是不能度量的,故④错误.综上可知,①③正确,故选B.
对于②,射线AB的端点是A,射线BA的端点是B,所以射线AB和射线BA不是同一条射线,故②错误;对于③,根据直线的表示方法可知,直线AB和直线BA是同一条直线,故③正确;
对于④,由射线的定义可知,射线是不能度量的,故④错误.综上可知,①③正确,故选B.
2.教材变式特色P55例1如图,已知线段AB,点C在AB上,点P在AB外.
(1)根据要求画出图形:画直线PA,画射线PB,连接PC.
(2)写出图中的所有线段.
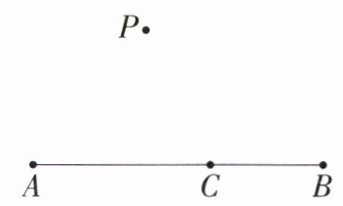
(1)根据要求画出图形:画直线PA,画射线PB,连接PC.
(2)写出图中的所有线段.

答案:
解析
(1)如图,直线PA,射线PB,线段PC即为所求.

(2)图中的所有线段为PA、PC、PB、AC、AB、CB.
解析
(1)如图,直线PA,射线PB,线段PC即为所求.

(2)图中的所有线段为PA、PC、PB、AC、AB、CB.
3.小明想在墙上钉一根细木条,要使细木条固定,至少需钉的钉子个数是 (
A.1
B.2
C.3
D.4
B
)A.1
B.2
C.3
D.4
答案:
B 根据“两点确定一条直线”的性质解答即可.
4.学科分类讨特色论思想过同一个平面内任意的四个点,可以确定____条直线.
答案:
答案 1或4或6
解析
(1)四点在同一条直线上,可确定1条直线,如图1;
(2)只有三个点在同一条直线上,可确定4条直线,如图2;
(3)任意三个点都不在同一条直线上,可确定6条直线,如图3.



答案 1或4或6
解析
(1)四点在同一条直线上,可确定1条直线,如图1;
(2)只有三个点在同一条直线上,可确定4条直线,如图2;
(3)任意三个点都不在同一条直线上,可确定6条直线,如图3.



5.「2022广西柳州中考」如图,从学校A到书店B有①②③④四条路线,其中最短的路线是 (
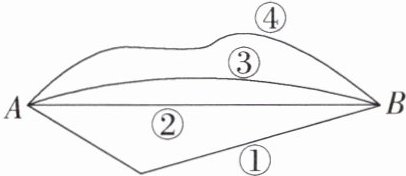
A.①
B.②
C.③
D.④
B
) 
A.①
B.②
C.③
D.④
答案:
B 由两点之间,线段最短知最短的路线是②.故选B.
6.下列说法正确的是 (
A.过A,B两点的直线的长度是A,B两点之间的距离
B.线段AB就是A,B两点之间的距离
C.在连接A,B两点的所有线中,最短的线的长度是A,B两点之间的距离
D.乘火车从上海到北京要走1462千米,这就是说上海站与北京站之间的距离是1462千米
C
)A.过A,B两点的直线的长度是A,B两点之间的距离
B.线段AB就是A,B两点之间的距离
C.在连接A,B两点的所有线中,最短的线的长度是A,B两点之间的距离
D.乘火车从上海到北京要走1462千米,这就是说上海站与北京站之间的距离是1462千米
答案:
C 直线是不可度量的;线段AB的长度是A,B两点之间的距离;1462千米是火车行驶的总路程,不是两站之间的距离,故选C.
7.新考向规律探究题「★☆」如图,3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,按照这样的规律,100条直线两两相交最多有
4950
个交点.
答案:
答案 4950
解析 2条直线相交有1个交点
3条直线相交最多有1+2=3=$\frac{3×(3-1)}{2}$个交点,
4条直线相交最多有1+2+3=6=$\frac{4×(4-1)}{2}$个交点,
5条直线相交最多有1+2+3+4=10=$\frac{5×(5-1)}{2}$个交点,
……
所以n条直线相交最多有$\frac{n(n-1)}{2}$个交点,
把n=100代入,得$\frac{n(n-1)}{2}$=$\frac{100×(100-1)}{2}$=4950.故100条直线相交最多有4950个交点.
解析 2条直线相交有1个交点
3条直线相交最多有1+2=3=$\frac{3×(3-1)}{2}$个交点,
4条直线相交最多有1+2+3=6=$\frac{4×(4-1)}{2}$个交点,
5条直线相交最多有1+2+3+4=10=$\frac{5×(5-1)}{2}$个交点,
……
所以n条直线相交最多有$\frac{n(n-1)}{2}$个交点,
把n=100代入,得$\frac{n(n-1)}{2}$=$\frac{100×(100-1)}{2}$=4950.故100条直线相交最多有4950个交点.
8.新课标几何直观【观察思考】如图,线段AB上有两个点C、D,分别以点A、B、C、D为端点的线段共有
【模型构建】若线段上有m个点(包括端点),则该线段上共有
【拓展应用】若有10支球队参加校级篮球比赛,比赛采用单循环制(即每支球队之间都要进行一场比赛),请你应用上述模型构建,求一共要进行多少场比赛.
6
条.【模型构建】若线段上有m个点(包括端点),则该线段上共有
$\frac{m(m-1)}{2}$
条线段.【拓展应用】若有10支球队参加校级篮球比赛,比赛采用单循环制(即每支球队之间都要进行一场比赛),请你应用上述模型构建,求一共要进行多少场比赛.
把10支球队看作直线上的10个点,每两支球队之间的一场比赛看作一条线段,由题意知,当m=10时,$\frac{m(m-1)}{2}$=$\frac{10×(10-1)}{2}$=45。故一共要进行45场比赛。
答案:
解析 【观察思考】3+2+1=6(条).故答案为6.
【模型构建】1+2+3+...+(m−1)=$\frac{m(m-1)}{2}$,故答案为$\frac{m(m-1)}{2}$.
【拓展应用】把10支球队看作直线上的10个点,每两支球队之间的一场比赛看作一条线段,由题意知,
当m=10时,$\frac{m(m-1)}{2}$=$\frac{10×(10-1)}{2}$=45.
故一共要进行45场比赛
【模型构建】1+2+3+...+(m−1)=$\frac{m(m-1)}{2}$,故答案为$\frac{m(m-1)}{2}$.
【拓展应用】把10支球队看作直线上的10个点,每两支球队之间的一场比赛看作一条线段,由题意知,
当m=10时,$\frac{m(m-1)}{2}$=$\frac{10×(10-1)}{2}$=45.
故一共要进行45场比赛
查看更多完整答案,请扫码查看


