《2025年5年中考3年模拟七年级数学上册苏科版》

14. 「2025江苏徐州沛县期中」(8分)将下列各数：$0$,$-\vert - 3\vert$,$(-1)^{2}$,$-2^{2}$,$3.5$在数轴上表示出来,并用“$＜$”把它们连接起来.

答案：
解析 如图

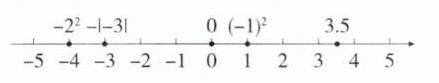
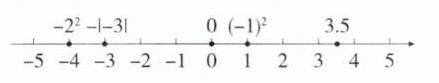
$-2^2$＜-|-3|＜0＜$(-1)^2$＜3.5.

15. (10分)有8筐白菜,以每筐25千克为标准,超过的千克数记为正数,不足的千克数记为负数,称重后的记录如下：
|筐号|1|2|3|4|5|6|7|8|
|与标准质量相比超过或不足的千克数|+1.5|-3|+2|-0.5|+1|-2|-2|-2.5|
(1)8筐白菜中,最接近25千克标准的是第4筐(填筐号),质量是24.5千克.
(2)8筐白菜中,最重的一筐比最轻的一筐重5千克.
(3)若白菜的售价为4元/千克,则出售这8筐白菜可卖多少钱？
1.5-3+2-0.5+1-2-2-2.5=-5.5(千克),(25×8-5.5)×4=194.5×4=778(元).答:出售这8筐白菜可卖778元.

答案：
(1)4;24.5.
详解:该组数据中,-0.5的绝对值最小,故最接近25千克标准的是第4筐,这筐白菜的质量为25-0.5=24.5(千克).
(2)5.
详解:[解法一]最重的一筐是第3筐,质量是25+2=27(千克),最轻的一筐是第2筐,质量是25-3=22(千克),所以最重的一筐比最轻的一筐重27-22=5(千克).
[解法二]2-(-3)=5(千克),所以最重的一筐比最轻的一筐重5千克.
(3)1.5-3+2-0.5+1-2-2-2.5=-5.5(千克),(25×8-5.5)×4=194.5×4=778(元).答:出售这8筐白菜可卖778元.

16. 「2025江苏宿迁沭阳月考」(14分)在解决数学问题的过程中,我们常用到分类讨论的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答问题.
【提出问题】三个有理数$a$,$b$,$c$满足abc＞0$,求$\frac{\vert a\vert}{a}+\frac{\vert b\vert}{b}+\frac{\vert c\vert}{c}$的值.【解决问题】解：由题意,得$a$,$b$,$c$三个有理数都为正数或其中一个为正数,另两个为负数.①当$a$,$b$,$c$都是正数,即$a＞0$,$b＞0$,$c＞0$时,$\frac{\vert a\vert}{a}+\frac{\vert b\vert}{b}+\frac{\vert c\vert}{c}= \frac{a}{a}+\frac{b}{b}+\frac{c}{c}= 1 + 1 + 1 = 3$；②当$a$,$b$,$c$中有一个为正数,另两个为负数时,不妨设$a＞0$,$b＜0$,$c＜0$,则$\frac{\vert a\vert}{a}+\frac{\vert b\vert}{b}+\frac{\vert c\vert}{c}= \frac{a}{a}+\frac{-b}{b}+\frac{-c}{c}= 1+(-1)+(-1)= -1$.综上所述,$\frac{\vert a\vert}{a}+\frac{\vert b\vert}{b}+\frac{\vert c\vert}{c}$的值为3或$-1$.【探究】请根据上面的解题思路解答下面的问题：(1)三个有理数$a$,$b$,$c$满足abc＜0$,求$\frac{\vert a\vert}{a}+\frac{\vert b\vert}{b}+\frac{\vert c\vert}{c}$的值.
根据题意可知,abc＜0,所以a,b,c三个数都是负数或其中一个为负数,另两个为正数.
①当a,b,c都是负数,即a＜0,b＜0,c＜0时,$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}$=$\frac{-a}{a}+\frac{-b}{b}+\frac{-c}{c}$=-1-1-1=-3.
②当a,b,c中有一个为负数,另两个为正数时,不妨设a＜0,b＞0,c＞0,则$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}$=$\frac{-a}{a}+\frac{b}{b}+\frac{c}{c}$=-1+1+1=1.综上,$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}$的值为-3或1.
(2)若$a$,$b$,$c$为三个不为0的有理数,且$\frac{a}{\vert a\vert}+\frac{b}{\vert b\vert}+\frac{c}{\vert c\vert}=-1$,求$\frac{abc}{\vert abc\vert}$的值.
因为a,b,c为三个不为0的有理数,且$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}$=-1,所以a,b,c三个数中,有两个为负数,一个为正数,所以abc＞0,故$\frac{abc}{|abc|}$=1.
(3)若$a$,$b$,$c$,$d$为四个不为0的有理数,则$\frac{a}{\vert a\vert}+\frac{b}{\vert b\vert}+\frac{c}{\vert c\vert}+\frac{d}{\vert d\vert}$的值为______.-4或-2或0或2或4

答案：
(1)根据题意可知,abc＜0,所以a,b,c三个数都是负数或其中一个为负数,另两个为正数.
①当a,b,c都是负数,即a＜0,b＜0,c＜0时,$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}$=$\frac{-a}{a}+\frac{-b}{b}+\frac{-c}{c}$=-1-1-1=-3.
②当a,b,c中有一个为负数,另两个为正数时,不妨设a＜0,b＞0,c＞0,则$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}$=$\frac{-a}{a}+\frac{b}{b}+\frac{c}{c}$=-1+1+1=1.综上,$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}$的值为-3或1.
(2)因为a,b,c为三个不为0的有理数,且$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}$=-1,所以a,b,c三个数中,有两个为负数,一个为正数,所以abc＞0,故$\frac{abc}{|abc|}$=1.
(3)根据题意可知,a,b,c,d为四个不为0的有理数,所以当a,b,c,d四个数都为正数时,$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}+\frac{d}{|d|}$=1+1+1+1=4;当a,b,c,d四个数中有一个为负数,三个为正数时,不妨设a为负数,b,c,d为正数,所以$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}+\frac{d}{|d|}$=-1+1+1+1=2;当a,b,c,d四个数中有两个为负数,两个为正数时,不妨设a,b为负数,c,d为正数,所以$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}+\frac{d}{|d|}$=-1-1+1+1=0;当a,b,c,d四个数中有三个为负数,一个为正数时,不妨设a,b,c为负数,d为正数,所以$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}+\frac{d}{|d|}$=-1-1-1+1=-2;当a,b,c,d四个数都为负数时,$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}+\frac{d}{|d|}$=-1-1-1-1=-4.综上,$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}+\frac{d}{|d|}$的值为-4或-2或0或2或4.