《2025年5年中考3年模拟七年级数学上册苏科版》

13.「2025江苏连云港海州期末」(8分)解方程:
(1)$2x+5= 3(x-1)$.
(2)$\frac {2x+1}{3}-\frac {5x-1}{6}= 1$.

答案：
(1)$2x+5=3(x-1)$,去括号,得$2x+5=3x-3$,移项,得$2x-3x=-3-5$,合并同类项,得$-x=-8$,系数化为1,得$x=8$.
(2)$\frac{2x+1}{3}-\frac{5x-1}{6}=1$,去分母,得$2(2x+1)-(5x-1)=6$,去括号,得$4x+2-5x+1=6$,移项、合并同类项,得$-x=3$,系数化为1,得$x=-3$.

14.「2025江苏苏州相城期末」(10分)我们规定:若关于x的一元一次方程$ax= b的解为x= b+a$,则称该方程为“和解方程”.例如:方程$2x= -4的解为x= -2,-2= -4+2$,则方程$2x= -4$为“和解方程”.
请根据上述规定解答下列问题:
(1)下列关于x的一元一次方程是“和解方程”的是(填序号).
①$3x= -5$;②$5x= -2$;③$-3x= \frac {9}{4}$.
③
(2)若关于x的一元一次方程$4x= 8a-12$是“和解方程”,求a的值.
解方程$4x=8a-12$,得$x=2a-3$,因为关于x的一元一次方程$4x=8a-12$是“和解方程”,所以$4+(8a-12)=2a-3$,解得$a=\frac{5}{6}$.

答案：
(1)③ 解方程$3x=-5$,得$x=-\frac{5}{3}$,因为$3+(-5)=-2≠-\frac{5}{3}$,所以方程$3x=-5$不是“和解方程”;解方程$5x=-2$,得$x=-\frac{2}{5}$,因为$5+(-2)=3≠-\frac{2}{5}$,所以方程$5x=-2$不是“和解方程”;解方程$-3x=\frac{9}{4}$,得$x=-\frac{3}{4}$,因为$-3+\frac{9}{4}=-\frac{3}{4}$,所以方程$-3x=\frac{9}{4}$是“和解方程”.故答案为③.
(2)解方程$4x=8a-12$,得$x=2a-3$,因为关于x的一元一次方程$4x=8a-12$是“和解方程”,所以$4+(8a-12)=2a-3$,解得$a=\frac{5}{6}$.

15.「2025江苏苏州姑苏期中」(10分)某打车软件计价内容含起步价(不超过3千米部分的里程费用)、里程费(超出3千米部分的里程费用)和时长费三部分,计价标准如下:

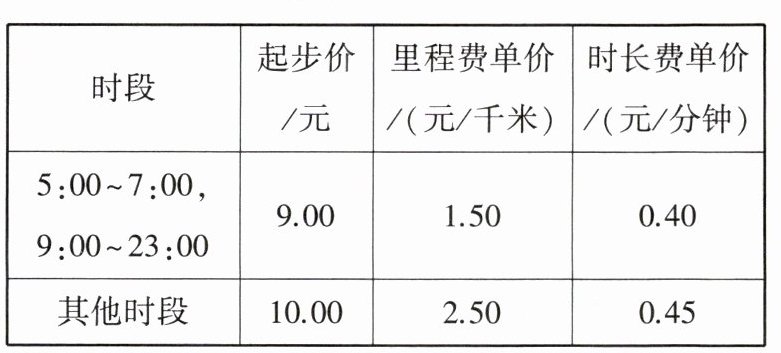
(1)张阿姨$17:00$用这款软件打车回家,里程为5千米,用时15分钟,求张阿姨需要支付的车费.
(2)李叔叔$8:00$用这款软件打车去距家2.8千米的单位,共支付车费14.5元,求李叔叔乘车的时长.

答案：
(1)根据题意,得$9+1.5×(5-3)+0.4×15=9+1.5×2+0.4×15=9+3+6=18$(元).答:张阿姨需要支付的车费为18元.
(2)设李叔叔乘车的时长为x分钟.根据题意,得$10+0.45x=14.5$,解得$x=10$.答:李叔叔乘车的时长为10分钟.

16.「2025江苏南京鼓楼期末」(12分)用A型机器和B型机器生产同样的产品,已知5台A型机器一天生产的产品装满8箱后还剩4个,7台B型机器一天生产的产品装满11箱后还剩1个,每台A型机器比B型机器一天多生产1个产品.
(1)求每箱装多少个产品.
(2)现需生产m箱产品,若用a台A型机器和b台B型机器同时生产,需要几天完成?(用含a,b,m的代数式表示)
(3)若每台A型机器一天的成本费用是110元,每台B型机器一天的成本费用是100元,可以运作的A型机器最少是18台,最多是20台,现要在一天内完成38箱产品的生产,请写出总成本的最小值.

答案：
(1)设每台A型机器一天生产x个产品,则每台B型机器一天生产$(x-1)$个产品,由题意,可得$\frac{5x-4}{8}=\frac{7(x-1)-1}{11}$,解得$x=20$,所以$\frac{5x-4}{8}=\frac{5×20-4}{8}=12$.答:每箱装12个产品.
(2)由
(1)可知,每台A型机器一天生产20个产品,故每台B型机器一天生产19个产品,所以若用a台A型机器和b台B型机器同时生产m箱产品,需要$\frac{12m}{20a+19b}$天完成.
(3)①当运作18台A型机器时,为满足生产要求,有$\frac{38×12-20×18}{19}=5\frac{1}{19}$,即还需要运作6台B型机器,所以总成本为$110×18+100×6=2580$(元).②当运作19台A型机器时,为满足生产要求,有$\frac{38×12-20×19}{19}=4$,即还需要运作4台B型机器,所以总成本为$110×19+100×4=2490$(元).③当运作20台A型机器时,为满足生产要求,有$\frac{38×12-20×20}{19}=2\frac{18}{19}$,即还需要运作3台B型机器,所以总成本为$110×20+100×3=2500$(元).因为2490元＜2500元＜2580元,所以要在一天内完成38箱产品的生产,总成本的最小值为2490元.