第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.如图,用同样大小的直角三角尺比较$∠CAD和∠EBF$的大小,下列判断正确的是 (
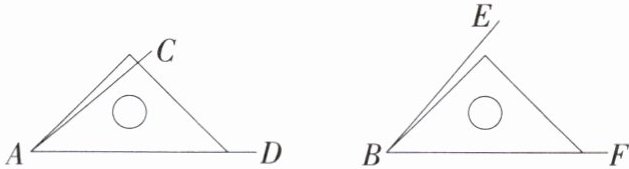
A.$∠CAD>∠EBF$
B.$∠CAD<∠EBF$
C.$∠CAD= ∠EBF$
D.没有量角器,无法确定
B
)
A.$∠CAD>∠EBF$
B.$∠CAD<∠EBF$
C.$∠CAD= ∠EBF$
D.没有量角器,无法确定
答案:
B 因为题图中的三角尺为等腰直角三角形,所以∠CAD<45°,∠EBF>45°,所以∠CAD<∠EBF,故选B.
2.已知$∠1的余角是50^{\circ },∠2的补角是140^{\circ }$,则$∠1与∠2$的大小关系是 (
A.$∠1>∠2$
B.$∠1<∠2$
C.$∠1= ∠2$
D.不能确定
C
)A.$∠1>∠2$
B.$∠1<∠2$
C.$∠1= ∠2$
D.不能确定
答案:
C 因为∠1的余角是50°,所以∠1 = 90° - 50° = 40°,因为∠2的补角是140°,所以∠2 = 180° - 140° = 40°,所以∠1 = ∠2.故选C.
3.比较大小:$20^{\circ }15'30''$
>
$20.25^{\circ }$.(填“>”“<”或“=”)
答案:
>
解析 因为20.25° = 20°15′,20°15'30">20°15′,所以20°15'30">20.25°.
解析 因为20.25° = 20°15′,20°15'30">20°15′,所以20°15'30">20.25°.
4.如图,用尺规作出了$∠NCB= ∠AOC$,作图痕迹中弧FG是 (
A.以点C为圆心,OD长为半径的弧
B.以点C为圆心,DM长为半径的弧
C.以点E为圆心,OD长为半径的弧
D.以点E为圆心,DM长为半径的弧
D
)A.以点C为圆心,OD长为半径的弧
B.以点C为圆心,DM长为半径的弧
C.以点E为圆心,OD长为半径的弧
D.以点E为圆心,DM长为半径的弧
答案:
D 根据作一个角等于已知角可得弧FG是以点E为圆心,DM长为半径的弧.故选D.
5.(1)用一副三角尺画出$135^{\circ }$的角.
(2)已知$∠1= 30^{\circ },∠2= 45^{\circ }$,画$∠AOB= 2∠1+∠2.$
(2)已知$∠1= 30^{\circ },∠2= 45^{\circ }$,画$∠AOB= 2∠1+∠2.$
答案:
解析
(1)如图1所示.

(2)如图2所示.

解析
(1)如图1所示.

(2)如图2所示.

6.「2024江苏苏州高新区期末」如图所示,已知点O是直线CD上的一点,$∠AOC= 30^{\circ }$,OB平分$∠AOD$,则$∠BOD$的度数是 (
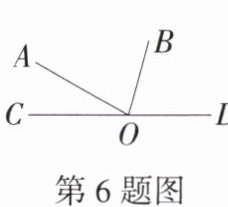
A.$75^{\circ }$
B.$65^{\circ }$
C.$55^{\circ }$
D.$45^{\circ }$
A
)
A.$75^{\circ }$
B.$65^{\circ }$
C.$55^{\circ }$
D.$45^{\circ }$
答案:
A 因为∠AOC = 30°,所以∠AOD = 180° - ∠AOC = 150°.因为OB平分∠AOD,所以∠BOD = $\frac{1}{2}$∠AOD = 75°.故选A.
7.如图,O是直线AB上一点,射线OD和射线OE分别平分$∠AOC和∠BOC$,若$∠COD= 62^{\circ }$,则$∠BOE= $
28
°.
答案:
28
解析 因为射线OD平分∠AOC,∠COD = 62°,所以∠AOC = 2∠COD = 124°,所以∠BOC = 180° - ∠AOC = 56°.因为射线OE平分∠BOC,所以∠BOE = $\frac{1}{2}$∠BOC = 28°.
解析 因为射线OD平分∠AOC,∠COD = 62°,所以∠AOC = 2∠COD = 124°,所以∠BOC = 180° - ∠AOC = 56°.因为射线OE平分∠BOC,所以∠BOE = $\frac{1}{2}$∠BOC = 28°.
8.如图,OD平分$∠BOC$,OE平分$∠AOC$.
(1)若$∠BOC= 60^{\circ },∠AOC= 40^{\circ }$,求$∠DOE$的度数.
(2)若$∠DOE= n^{\circ }$,求$∠AOB$的度数.
(3)若$∠DOE+∠AOB= 180^{\circ }$,求$∠AOB与∠DOE$的度数.
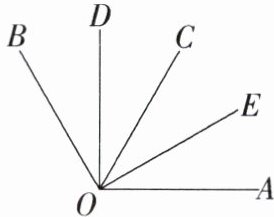
(1)若$∠BOC= 60^{\circ },∠AOC= 40^{\circ }$,求$∠DOE$的度数.
(2)若$∠DOE= n^{\circ }$,求$∠AOB$的度数.
(3)若$∠DOE+∠AOB= 180^{\circ }$,求$∠AOB与∠DOE$的度数.

答案:
解析
(1)因为OD平分∠BOC,∠BOC = 60°,所以∠COD = $\frac{1}{2}$∠BOC = 30°,同理可得∠COE = 20°,所以∠DOE = ∠COD + ∠COE = 30° + 20° = 50°.
(2)因为OD平分∠BOC,所以∠BOC = 2∠DOC.同理可得∠AOC = 2∠COE.因为∠AOB = ∠BOC + ∠AOC,所以∠AOB = 2∠DOC + 2∠COE = 2(∠DOC + ∠COE) = 2∠DOE = 2n°.
(3)因为∠AOB = 2∠DOE,∠DOE + ∠AOB = 180°,所以∠DOE + 2∠DOE = 180°,所以∠DOE = 60°,所以∠AOB = 120°.
(1)因为OD平分∠BOC,∠BOC = 60°,所以∠COD = $\frac{1}{2}$∠BOC = 30°,同理可得∠COE = 20°,所以∠DOE = ∠COD + ∠COE = 30° + 20° = 50°.
(2)因为OD平分∠BOC,所以∠BOC = 2∠DOC.同理可得∠AOC = 2∠COE.因为∠AOB = ∠BOC + ∠AOC,所以∠AOB = 2∠DOC + 2∠COE = 2(∠DOC + ∠COE) = 2∠DOE = 2n°.
(3)因为∠AOB = 2∠DOE,∠DOE + ∠AOB = 180°,所以∠DOE + 2∠DOE = 180°,所以∠DOE = 60°,所以∠AOB = 120°.
9.「2024江苏盐城建湖二模,★☆」如图,在$4×4$的正方形网格中,记$∠ABF= α,∠FCH= β,∠DGE= γ$,则α,β,γ的大小关系是 ( )
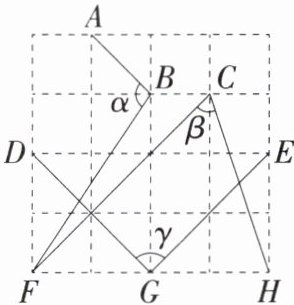
A.$β<α<γ$
B.$β<γ<α$
C.$α<γ<β$
D.$α<β<γ$

A.$β<α<γ$
B.$β<γ<α$
C.$α<γ<β$
D.$α<β<γ$
答案:
B 由题图知,∠FBG<45°,所以α = ∠ABF = 180° - 45° - ∠FBG>90°;由题图知,∠DGF = 45°,∠EGH = 45°,所以γ = ∠DGE = 180° - ∠DGF - ∠EGH = 180° - 45° - 45° = 90°.

如图,取格点M,连接CM,则∠MCH<45°,∠MCF = 45°,所以β = ∠FCH = ∠MCF + ∠MCH = 45° + ∠MCH<90°,所以β<γ<α.故选B.
B 由题图知,∠FBG<45°,所以α = ∠ABF = 180° - 45° - ∠FBG>90°;由题图知,∠DGF = 45°,∠EGH = 45°,所以γ = ∠DGE = 180° - ∠DGF - ∠EGH = 180° - 45° - 45° = 90°.

如图,取格点M,连接CM,则∠MCH<45°,∠MCF = 45°,所以β = ∠FCH = ∠MCF + ∠MCH = 45° + ∠MCH<90°,所以β<γ<α.故选B.
查看更多完整答案,请扫码查看


