第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.「2025 江苏泰州姜堰期末」下列实物中,能抽象成圆柱的是(
C
)
答案:
1.C A.能抽象成六棱柱,不合题意;B.能抽象成球,不合题意;C.能抽象成圆柱,符合题意;D.能抽象成圆锥,不合题意.故选C.
2.「2025 江苏扬州仪征期末」下列四个几何体中,是四棱锥的是(
A
)
答案:
2.A 四棱锥是底面为四边形的锥体,因此选项A中的几何体符合题意.故选A.
3.观察图中所示的八个几何体。
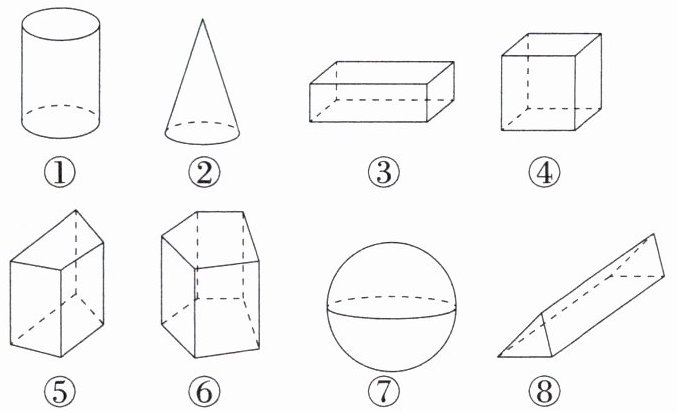
(1)依次写出这八个几何体的名称。
(2)按柱体、锥体、球体对上述几何体进行分类(填序号)。

(1)依次写出这八个几何体的名称。
(2)按柱体、锥体、球体对上述几何体进行分类(填序号)。
答案:
3.解析
(1)圆柱;圆锥;长方体;正方体;四棱柱;五棱柱;球;三棱柱.
(2)柱体有①③④⑤⑥⑧,锥体有②,球体有⑦.方法解读 将几何体分类时,应做到不重不漏,每个几何体只能属于一个类别.
(1)圆柱;圆锥;长方体;正方体;四棱柱;五棱柱;球;三棱柱.
(2)柱体有①③④⑤⑥⑧,锥体有②,球体有⑦.方法解读 将几何体分类时,应做到不重不漏,每个几何体只能属于一个类别.
4.「2025 江苏泰州泰兴期末」若一个棱柱有 12 个顶点,则这个棱柱有
8
个面。
答案:
4.答案 8解析 因为棱柱有12个顶点,所以这个棱柱是六棱柱,六棱柱有8个面,故答案为8.
5.(1)三棱锥有
(2)
(3)一个棱锥的棱数是 100,则这个棱锥是
6
条棱,四棱锥有8
条棱,五棱锥有10
条棱。(2)
十五
棱锥有 30 条棱。(3)一个棱锥的棱数是 100,则这个棱锥是
五十
棱锥。
答案:
5.答案
(1)6;8;10
(2)十五
(3)五十
(1)6;8;10
(2)十五
(3)五十
6.「2025 江苏镇江句容期末,★☆」如图所示的为小文同学的几何体素描作品,该作品中不存在的几何体为(

A.棱柱
B.球
C.圆柱
D.棱锥
D
)
A.棱柱
B.球
C.圆柱
D.棱锥
答案:
6.D 由题图可得小文同学的几何体素描作品中有棱柱,球,圆柱,圆锥,没有棱锥,故选D.
7.「2024 上海浦东新区期末,★☆」若将一个长方体的一个角切去,则所得到的几何体的顶点和棱的数量最多分别为( )
A.8 个顶点,13 条棱
B.10 个顶点,15 条棱
C.8 个顶点,15 条棱
D.10 个顶点,13 条棱
A.8 个顶点,13 条棱
B.10 个顶点,15 条棱
C.8 个顶点,15 条棱
D.10 个顶点,13 条棱
答案:
7.B 将一个长方体的一个角切去后,剩下的几何体可能有7个顶点、12条棱、7个面或8个顶点、13条棱、7个面或9个顶点、14条棱、7个面或10个顶点、15条棱、7个面,如图所示,则剩下的几何体最多有10个顶点,15条棱,故选B.
7.B 将一个长方体的一个角切去后,剩下的几何体可能有7个顶点、12条棱、7个面或8个顶点、13条棱、7个面或9个顶点、14条棱、7个面或10个顶点、15条棱、7个面,如图所示,则剩下的几何体最多有10个顶点,15条棱,故选B.

8.「2024 江苏泰州高港期末,★☆」若一个棱柱有 12 个顶点,且所有侧棱长的和为 30cm,则每条侧棱长为
5
cm。
答案:
8.答案 5解析 由这个棱柱有12个顶点,可知它是六棱柱,所以有6条侧棱,又因为所有侧棱长的和为30cm,所以每条侧棱长为30÷6 = 5(cm).
9.新 考向 「2025 江苏苏州姑苏月考,★☆」观察如图所示的几何体,回答下列问题:
(1)填写下表:
|序号|图形名称|底面边数|侧面数|侧棱数|顶点数|
|①|三棱柱|
|②|四棱柱|
|③|六棱柱|
(2)根据(1)中的结果,你能得出棱柱的侧面数、侧棱数、顶点数与棱柱底面边数之间各有什么关系吗?
(3)根据(2)中的猜想,直接写出二十棱柱的侧面数、侧棱数、顶点数。
(1)填写下表:
|序号|图形名称|底面边数|侧面数|侧棱数|顶点数|
|①|三棱柱|
3
|3
|3
|6
||②|四棱柱|
4
|4
|4
|8
||③|六棱柱|
6
|6
|6
|12
|(2)根据(1)中的结果,你能得出棱柱的侧面数、侧棱数、顶点数与棱柱底面边数之间各有什么关系吗?
棱柱的侧面数 = 棱柱底面边数,棱柱的侧棱数 = 棱柱底面边数,棱柱的顶点数 = 棱柱底面边数×2.
(3)根据(2)中的猜想,直接写出二十棱柱的侧面数、侧棱数、顶点数。
二十棱柱的侧面数是20,侧棱数是20,顶点数是40.
答案:
9.解析
(1)填表如下:
序号 图形名称 底面边数 侧面数 侧棱数 顶点数
① 三棱柱 3 3 3 6
② 四棱柱 4 4 4 8
③ 六棱柱 6 6 6 12
(2)棱柱的侧面数 = 棱柱底面边数,棱柱的侧棱数 = 棱柱底面边数,棱柱的顶点数 = 棱柱底面边数×2.
(3)二十棱柱的侧面数是20,侧棱数是20,顶点数是40.
(1)填表如下:
序号 图形名称 底面边数 侧面数 侧棱数 顶点数
① 三棱柱 3 3 3 6
② 四棱柱 4 4 4 8
③ 六棱柱 6 6 6 12
(2)棱柱的侧面数 = 棱柱底面边数,棱柱的侧棱数 = 棱柱底面边数,棱柱的顶点数 = 棱柱底面边数×2.
(3)二十棱柱的侧面数是20,侧棱数是20,顶点数是40.
查看更多完整答案,请扫码查看


