《2025年5年中考3年模拟七年级数学上册苏科版》

1. 「2025江苏盐城亭湖月考」“鸣语既过渐细微,映空摇飏如丝飞”是唐代诗人杜甫作品《雨不绝》中的诗句,意为喧哗的雨已经过去,逐渐变得细微,映着天空摇漾如丝的细雨飘飞.诗中描写雨滴下来形成雨丝,用数学语言解释这一现象为点动成线.

答案： 答案 点动成线
解析 把雨滴抽象为点，雨丝抽象为线，据此可用数学语言解释这一现象属于点动成线.

2. 「2025山东济宁任城月考」如图,第二行的图形绕虚线旋转一周,便能形成第一行的某个几何体,用线连一连.

答案：
解析 如图所示:

方法归纳 平面图形的旋转，要抓住平面图形的边界线的运动，以及旋转前图形的边界线与旋转轴的角度来想象所形成的立体图形的情况.

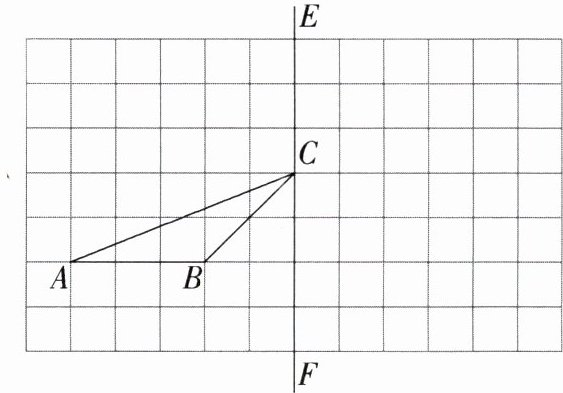
3. 如图,在由边长为1的小正方形组成的网格中有一个△ABC,按要求回答下列问题：
(1)△ABC的面积为______.
(2)画出将△ABC向右平移6格,再向上平移3格后的$△A_1B_1C_1.$
(3)画出△ABC绕点B顺时针旋转90°后的图形$△A_2BC_2.$
(4)画出△ABC沿直线EF翻折后的图形$△A_3B_3C.$

答案：
解析
(1)3.
(2)如图,$\triangle A_{1}B_{1}C_{1}$即为所求.
(3)如图,$\triangle A_{2}BC_{2}$即为所求.
(4)如图,$\triangle A_{3}B_{3}C$即为所求.

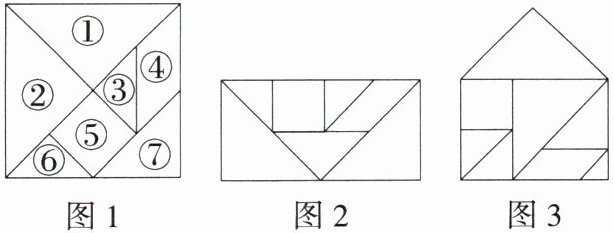
4. 七巧板是我国祖先的一项卓越创造,图2和图3中有一幅是小明用如图1所示的七巧板拼成的,另一幅则不是.请选出不是小明用图1所示的七巧板拼成的那幅图,并说明选择的理由.

答案： 解析 七巧板有5个等腰直角三角形(其中有大、小两对完全一样的三角形);一个正方形;一个平行四边形.根据这些图形的性质可知，题图2是由七巧板拼成的，题图3不是，题图3中有6个等腰直角三角形.
方法解读 解用“七巧板”拼图问题的方法
解用“七巧板”拼图问题时，一般先熟悉“七巧板”的结构:五个等腰直角三角形，其中有两对能完全重合;一个正方形;一个平行四边形.根据它的结构想象可能拼接的方式，然后利用自备的“七巧板”学具动手尝试操作，直到拼出题目要求的图形为止.

5. 「2025福建厦门海沧期中,★☆」如图,将长方形纸片先沿虚线AB向右对折,接着将对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的图形是(D)

A.
B.

答案： 5.D 动手操作即可得到答案.

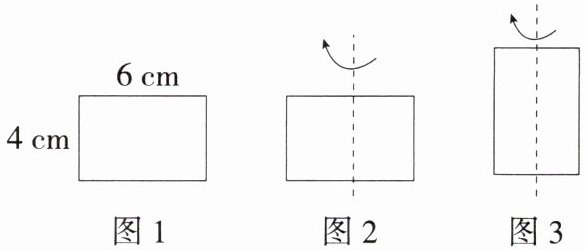
6. 「2025江苏无锡宜兴月考,★☆」如图1,有一个长6cm,宽4cm的长方形纸板,现要求以其一组对边中点所在直线为轴旋转180°,可按两种方案进行操作.
方案一：以较长的一组对边中点所在直线为轴旋转,如图2.
方案二：以较短的一组对边中点所在直线为轴旋转,如图3.
(1)上述操作能形成的几何体是圆柱,说明的事实是面动成体.
(2)请通过计算说明哪种方案得到的几何体的体积大.

方案一:$\pi × 3^{2}× 4=36\pi (\unit{cm^{3}})$,
方案二:$\pi × 2^{2}× 6=24\pi (\unit{cm^{3}})$,
因为$36\pi ＞24\pi $,
所以方案一得到的几何体的体积大.

答案： 解析
(1)以一组对边中点所在直线为轴旋转，能形成的几何体是圆柱，说明的事实是面动成体.故答案为圆柱;面动成体.
(2)方案一:$\pi × 3^{2}× 4=36\pi (\unit{cm^{3}})$,
方案二:$\pi × 2^{2}× 6=24\pi (\unit{cm^{3}})$,
因为$36\pi ＞24\pi $,
所以方案一得到的几何体的体积大.