第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
21. 「2025江苏宿迁宿豫期末」(8分)出租车司机王师傅某天下午的营运都是在东西方向的洪泽湖路上进行的,如果规定向东行驶为正,他这天下午行车的里程(单位:千米)如下:+4,-8,+5,+2,-11,+3,-2,-6.
(1)若把王师傅下午出发地记为0,他将最后一名乘客送到目的地时,王师傅距下午出发地有多远? 他最后在出发地的什么方向?
(2)如果汽车耗油量为0.05升/千米,那么这天下午汽车共耗油多少升?
(1)若把王师傅下午出发地记为0,他将最后一名乘客送到目的地时,王师傅距下午出发地有多远? 他最后在出发地的什么方向?
(2)如果汽车耗油量为0.05升/千米,那么这天下午汽车共耗油多少升?
答案:
(1)$+4-8+5+2-11+3-2-6=-13$(千米).故他将最后一名乘客送到目的地时,距下午出发地有13千米,他最后在出发地的西边.
(2)$(4+|-8|+5+2+|-11|+3+|-2|+|-6|)×0.05=2.05$(升).答:这天下午汽车共耗油2.05升
(1)$+4-8+5+2-11+3-2-6=-13$(千米).故他将最后一名乘客送到目的地时,距下午出发地有13千米,他最后在出发地的西边.
(2)$(4+|-8|+5+2+|-11|+3+|-2|+|-6|)×0.05=2.05$(升).答:这天下午汽车共耗油2.05升
22. 「2025江苏盐城盐都期中」(10分)数学中的许多规律不仅可以通过数的运算发现,也可以通过图形的面积发现.
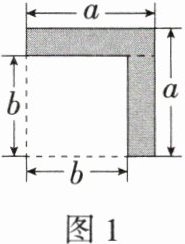
(1)如图1,在边长为a的正方形纸片上剪去一个边长为$b(b<a)$的小正方形.小明和小红分别用了两种不同的方法计算图中阴影部分的面积.小明的方法:若阴影部分看成大正方形与小正方形的面积差,则阴影部分的面积用代数式表示为
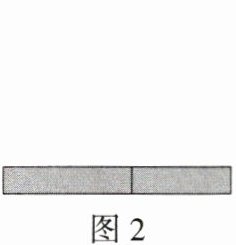
小红的方法:若将图1中的阴影部分沿虚线剪开拼成新的长方形(如图2),则阴影部分的面积用代数式表示为
(2)【发现规律】
猜想:$a+b,a-b,a^2-b^2$这三个代数式之间的数量关系是
(3)【运用规律】
运用上述规律计算:$50^2-49^2+48^2-47^2+46^2-45^2+…+2^2-1$.
(1)如图1,在边长为a的正方形纸片上剪去一个边长为$b(b<a)$的小正方形.小明和小红分别用了两种不同的方法计算图中阴影部分的面积.小明的方法:若阴影部分看成大正方形与小正方形的面积差,则阴影部分的面积用代数式表示为
$a^2-b^2$
;小红的方法:若将图1中的阴影部分沿虚线剪开拼成新的长方形(如图2),则阴影部分的面积用代数式表示为
$(a+b)(a-b)$
.

(2)【发现规律】
猜想:$a+b,a-b,a^2-b^2$这三个代数式之间的数量关系是
$a^2-b^2=(a+b)(a-b)$
.(3)【运用规律】
运用上述规律计算:$50^2-49^2+48^2-47^2+46^2-45^2+…+2^2-1$.
$50^2-49^2+48^2-47^2+46^2-45^2+\cdots+2^2-1=(50^2-49^2)+(48^2-47^2)+(46^2-45^2)+\cdots+(2^2-1)=(50+49)×(50-49)+(48+47)×(48-47)+(46+45)×(46-45)+\cdots+(2+1)×(2-1)=50+49+48+47+46+45+\cdots+2+1=\frac{50×(50+1)}{2}=1275$
答案:
(1)$a^2-b^2$;$(a+b)(a-b)$.
(2)$a^2-b^2=(a+b)(a-b)$.
(3)$50^2-49^2+48^2-47^2+46^2-45^2+\cdots+2^2-1=(50^2-49^2)+(48^2-47^2)+(46^2-45^2)+\cdots+(2^2-1)=(50+49)×(50-49)+(48+47)×(48-47)+(46+45)×(46-45)+\cdots+(2+1)×(2-1)=50+49+48+47+46+45+\cdots+2+1=\frac{50×(50+1)}{2}=1275$
(1)$a^2-b^2$;$(a+b)(a-b)$.
(2)$a^2-b^2=(a+b)(a-b)$.
(3)$50^2-49^2+48^2-47^2+46^2-45^2+\cdots+2^2-1=(50^2-49^2)+(48^2-47^2)+(46^2-45^2)+\cdots+(2^2-1)=(50+49)×(50-49)+(48+47)×(48-47)+(46+45)×(46-45)+\cdots+(2+1)×(2-1)=50+49+48+47+46+45+\cdots+2+1=\frac{50×(50+1)}{2}=1275$
23. 新考向 (12分)同样大小的黑色棋子按如图所示的规律摆放:
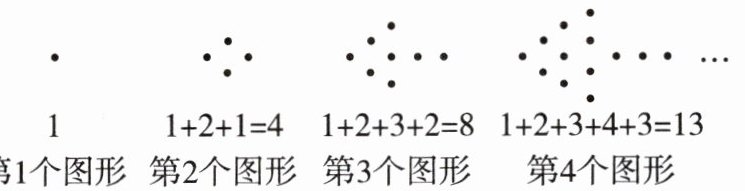
(1)第5个图形中有
(2)第$(n+2)$个图形比第n个图形多多少颗黑色棋子? (用含n的代数式表示)

(1)第5个图形中有
19
颗黑色棋子;第8个图形比第6个图形多17
颗黑色棋子.(填数字)(2)第$(n+2)$个图形比第n个图形多多少颗黑色棋子? (用含n的代数式表示)
由(1)得,第n个图形中有$[1+2+\cdots+n+(n-1)]$颗黑色棋子,第$(n+2)$个图形中有$[1+2+\cdots+n+(n+1)+(n+2)+(n+1)]$颗黑色棋子,$[1+2+\cdots+n+(n+1)+(n+2)+(n+1)]-[1+2+\cdots+n+(n-1)]=(n+1)+(n+2)+(n+1)-(n-1)=2n+5$,所以第$(n+2)$个图形比第n个图形多$(2n+5)$颗黑色棋子
答案:
(1)19;17.
(2)由
(1)得,第n个图形中有$[1+2+\cdots+n+(n-1)]$颗黑色棋子,第$(n+2)$个图形中有$[1+2+\cdots+n+(n+1)+(n+2)+(n+1)]$颗黑色棋子,$[1+2+\cdots+n+(n+1)+(n+2)+(n+1)]-[1+2+\cdots+n+(n-1)]=(n+1)+(n+2)+(n+1)-(n-1)=2n+5$,所以第$(n+2)$个图形比第n个图形多$(2n+5)$颗黑色棋子
(1)19;17.
(2)由
(1)得,第n个图形中有$[1+2+\cdots+n+(n-1)]$颗黑色棋子,第$(n+2)$个图形中有$[1+2+\cdots+n+(n+1)+(n+2)+(n+1)]$颗黑色棋子,$[1+2+\cdots+n+(n+1)+(n+2)+(n+1)]-[1+2+\cdots+n+(n-1)]=(n+1)+(n+2)+(n+1)-(n-1)=2n+5$,所以第$(n+2)$个图形比第n个图形多$(2n+5)$颗黑色棋子
24. 「2025江苏常熟期中」(12分)数轴上点A表示的数为-4,点B表示的数为8,点C表示的数为-1.
(1)如图1,若将数轴沿点C折叠,点A落在数轴上的点$A'$处,则点$A'$表示的数为______.
(2)如图2,点P、点Q在数轴上运动.点P从点A出发,以每秒1个单位长度的速度向左运动,点Q从点C出发,以每秒a个单位长度的速度向右运动,记P,Q两点之间的距离为$d_1$,B,Q两点之间的距离为$d_2$,若P,Q两点同时出发,经过3秒后,$d_1-2d_2= 0$,试求a的值.

(1)
(2)
(1)如图1,若将数轴沿点C折叠,点A落在数轴上的点$A'$处,则点$A'$表示的数为______.
(2)如图2,点P、点Q在数轴上运动.点P从点A出发,以每秒1个单位长度的速度向左运动,点Q从点C出发,以每秒a个单位长度的速度向右运动,记P,Q两点之间的距离为$d_1$,B,Q两点之间的距离为$d_2$,若P,Q两点同时出发,经过3秒后,$d_1-2d_2= 0$,试求a的值.

(1)
2
(2)
经过3秒后,点P表示的数是$-4-3=-7$,点Q表示的数是$-1+3a$,当点Q在点B的左侧时,因为$d_1-2d_2=0$,所以$-1+3a-(-7)-2[8-(-1+3a)]=0$,所以$a=\frac{4}{3}$;当点Q在点B的右侧时,因为$d_1-2d_2=0$,所以$-1+3a-(-7)-2(-1+3a-8)=0$,所以$a=8$.综上,a的值为$\frac{4}{3}$或8
答案:
(1)2.
(2)经过3秒后,点P表示的数是$-4-3=-7$,点Q表示的数是$-1+3a$,当点Q在点B的左侧时,因为$d_1-2d_2=0$,所以$-1+3a-(-7)-2[8-(-1+3a)]=0$,所以$a=\frac{4}{3}$;当点Q在点B的右侧时,因为$d_1-2d_2=0$,所以$-1+3a-(-7)-2(-1+3a-8)=0$,所以$a=8$.综上,a的值为$\frac{4}{3}$或8
(1)2.
(2)经过3秒后,点P表示的数是$-4-3=-7$,点Q表示的数是$-1+3a$,当点Q在点B的左侧时,因为$d_1-2d_2=0$,所以$-1+3a-(-7)-2[8-(-1+3a)]=0$,所以$a=\frac{4}{3}$;当点Q在点B的右侧时,因为$d_1-2d_2=0$,所以$-1+3a-(-7)-2(-1+3a-8)=0$,所以$a=8$.综上,a的值为$\frac{4}{3}$或8
查看更多完整答案,请扫码查看


