《2025年5年中考3年模拟七年级数学上册苏科版》

11.「2024 山东临沂临沭期中,」小明周日准备完成老师布置的作业：化简$(□x^{2} + 4x + 3) - (4x + 5x^{2} + 2)$,但发现$x^{2}$的系数“$□$”印刷不清楚.
(1) 他把“$□$”猜成 3,请你化简$(3x^{2} + 4x + 3) - (4x + 5x^{2} + 2)$.
(2) 小明妈妈说：“我看到此题的标准答案是$2x^{2} + 1$.”请你通过计算说明题中“$□$”是多少.

答案：
(1)(3x²+4x+3)-(4x+5x²+2)=3x²+4x+3-4x-5x²-2=-2x²+1.
(2)(2x²+1)+(4x+5x²+2)=2x²+1+4x+5x²+2=7x²+4x+3.所以题中“□”是7.

12. 运算能力 将式子$3x + (2x - x) = 3x + 2x - x$,$3x - (2x - x) = 3x - 2x + x$分别反过来,你得到两个怎样的等式？
$3x + 2x - x = 3x + (2x - x)$，$3x - 2x + x = 3x - (2x - x)$
【探究】比较你得到的等式,你能总结添括号的法则吗？
去括号与添括号是互逆的,括号前边是“+”号,移进括号的项无需变号;括号前边是“-”号,移进括号的项需要变号.
【应用】根据上面你总结出的添括号法则,不改变多项式$x^{3} - 3x^{2} + 3x - 1$的值,把它的后两项放在：
①前面带有“$+$”号的括号里；
$x^{3} - 3x^{2} + (3x - 1)$
②前面带有“$-$”号的括号里.
$x^{3} - 3x^{2} - (-3x + 1)$
【拓展】若$2m + n = 4$,则$6 - 2m - n$的值为______.
2

答案： 【探究】去括号与添括号是互逆的,括号前边是“+”号,移进括号的项无需变号;括号前边是“-”号,移进括号的项需要变号.【应用】①x³-3x²+3x-1=x³-3x²+(3x-1).②x³-3x²+3x-1=x³-3x²-(-3x+1).【拓展】2.详解:因为2m+n=4,所以6-2m-n=6-(2m+n)=6-4=2.

1.「2024 江苏无锡期末」如图,数轴上点$A$,$B$,$C所表示的数分别为a$,$b$,$c$,化简：$|a| + |c - b| - |a + b - c| = $0.

答案： 答案 0 解析 根据题意得a＜0＜b＜c,所以c-b＞0,a+b-c＜0,所以|a|+|c-b|-|a+b-c|=-a+(c-b)+(a+b-c)=-a+c-b+a+b-c=0.

2. 已知有理数$a$,$b$,$c$在数轴上对应的点的位置如图所示. 解答下列各题：
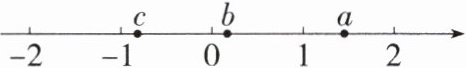
(1) 用“$＞$”或“$＜$”填空：
$a - b$＞$0$,$b - c$＞$0$,$c - a$＜$0$,$b + c$＜$0$.
(2) 化简：$|a - b| + |b - c| - |c - a| + |b + c|$.

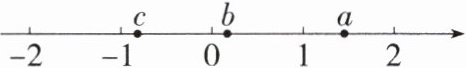
$-b - c$

答案：
(1)根据题中数轴可知,-1＜c＜0＜b＜1＜a＜2,且|c|＞|b|,所以a-b＞0,b-c＞0,c-a＜0,b+c＜0.故答案为＞;＞;＜;＜.
(2)原式=(a-b)+(b-c)+(c-a)-(b+c)=a-b+b-c+c-a-b-c=-b-c.

3. 有理数$a$,$b$,$c$在数轴上对应的点的位置如图所示,先化简,再求值：$|b - a| - 2|c + a| + |c - b| + |b + c|$,其中$a = -\frac{2}{3}$,$b = -3$,$c = \frac{5}{4}$.

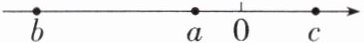
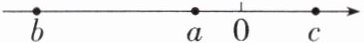
答案： 由题中数轴可知,b＜a＜0＜c,且|b|＞|c|＞|a|,则原式=-(b-a)-2(c+a)+(c-b)-(b+c)=-b+a-2c-2a+c-b-b-c=-a-3b-2c.当a=-2/3,b=-3,c=5/4时,原式=-(-2/3)-3×(-3)-2×5/4=43/6.