《2025年5年中考3年模拟七年级数学上册苏科版》

11. 「2025江苏无锡锡山月考,★☆」下面两个量中,不具有相反意义的是(A)
A.进三个球和输三场比赛
B.浪费1t水和节约1t水
C.盈利400元和亏损400元
D.上升50m和下降50m

答案： 【解析】：
本题考查对具有相反意义的量的识别。具有相反意义的量需要满足两个条件：一是它们表示的意义相反，二是它们都是数量，并且可以用正负数来表示。
A选项中，“进三个球”表示的是进球的数量，而“输三场比赛”表示的是输掉比赛的场数，这两个量并不是同一类量，并且它们之间并不构成相反意义。进球的反义词应该是未进球或者丢球，而不是输比赛。
B选项中，“浪费1t水”和“节约1t水”是相反意义的量，一个表示消耗了资源，另一个表示节省了资源。
C选项中，“盈利400元”和“亏损400元”也是相反意义的量，一个表示赚取了利润，另一个表示发生了损失。
D选项中，“上升50m”和“下降50m”同样是相反意义的量，一个表示位置的提高，另一个表示位置的降低。
因此，不具有相反意义的是A选项。
【答案】：
A

12. 「2025江苏连云港海州实验中学期中,★☆」下列关于有理数的描述：
①有限小数和无限循环小数都是有理数；
②0是非负有理数；
③0既不是正数,也不是负数,由此可知0不是有理数；
④一个有理数如果不是整数,那么它一定是分数。其中正确的个数是(C)
A.1
B.2
C.3
D.4

答案： 解：①有限小数和无限循环小数都是有理数，正确；
②0是非负有理数，正确；
③0既不是正数，也不是负数，但0是有理数，错误；
④一个有理数如果不是整数，那么它一定是分数，正确。
正确的个数是3个。
答案：C

13. 「2025江苏宜兴实验教育集团月考,★☆」一种面粉的质量标识为“$25\pm0.25$千克”,则下列面粉质量中合格的是(C)
A.24.70千克
B.25.30千克
C.24.80千克
D.25.51千克

答案： 【解析】：
本题主要考察了对正负数的理解和应用。题目中的“$25\pm0.25$千克”表示面粉的质量在$25-0.25=24.75$千克到$25+0.25=25.25$千克之间都是合格的。我们需要从选项中找出在这个范围内的面粉质量。
A选项：$24.70\lt 24.75$，不在合格范围内，故A错误；
B选项：$25.30\gt 25.25$，不在合格范围内，故B错误；
C选项：$24.75\lt 24.80\lt 25.25$，在合格范围内，故C正确；
D选项：$25.51\gt 25.25$，不在合格范围内，故D错误。
所以，正确答案是C。
【答案】：C

14. 「2023江苏泰州姜堰期中改编,★☆」下表记录了体育课上某小组6名男生引体向上的个数情况：
|引体向上的个数|5|6|10|8|9|12|
以9个为标准,超过的个数记作正数,不足的个数记作负数,他们对应的引体向上个数分别记作什么？

答案： 【解析】：
这是一个正负数在实际问题中的应用问题。
首先，需要明确标准数量是9个。
然后，需要计算每个学生的引体向上数量与标准数量的差值。
如果学生的引体向上数量超过9个，那么差值就是正数；
如果不足9个，差值就是负数；
如果刚好9个，差值就是0。
【答案】：
首先，我们明确标准是9个。
对于第一个学生，他做了5个引体向上，与标准的差值为$5 - 9 = -4$，所以记作-4；
第二个学生做了6个，与标准的差值为$6 - 9 = -3$，所以记作-3；
第三个学生做了10个，与标准的差值为$10 - 9 = 1$，所以记作+1；
第四个学生做了8个，与标准的差值为$8 - 9 = -1$，所以记作-1；
第五个学生做了9个，与标准的差值为$9 - 9 = 0$，所以记作0；
第六个学生做了12个，与标准的差值为$12 - 9 = 3$，所以记作+3。
故他们对应的引体向上个数分别记作-4，-3，+1，-1，0，+3。

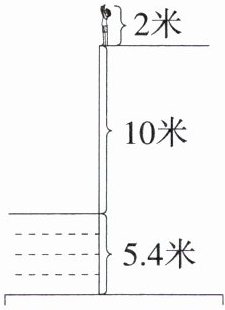
15. 「2023江苏泰州月考,★☆」如图,一名跳水运动员参加10米跳台的跳水比赛(10米跳台是指跳台离水面的高度为10米),这名运动员举高手臂时身长为2米,水池深5.4米。(规定向上为正)
(1)若以水面为基准,则这名运动员指尖的高度及池底的深度分别如何表示？
(2)若以跳台为基准,则池底的深度与水面的高度分别如何表示？
]

答案： 【解析】：本题主要考查正数和负数的应用，以及如何根据基准来表示其他物体的位置。
(1)若以水面为基准，向上为正：
由于跳台离水面的高度为10米，运动员举高手臂时身长为2米，
因此运动员指尖的高度在水面之上$10+2=12(米)$，
所以，以水面为基准，运动员指尖的高度表示为$+12$米。
池底在水面之下$5.4$米，所以池底的深度表示为$-5.4$米。
(2)若以跳台为基准，向下为负，向上为正：
池底在跳台之下$10+5.4=15.4(米)$，
所以池底的深度表示为$-15.4$米。
水面在跳台之下$10$米，所以水面的高度表示为$-10$米，
或者表示为跳台高度（$0$米）向下$10$米，即$-10$米。
【答案】：
(1)以水面为基准，则这名运动员指尖的高度表示为$+12$米，池底的深度表示为$-5.4$米。
(2)以跳台为基准，则池底的深度表示为$-15.4$米，水面的高度表示为$-10$米。

16. 新 推理能力 将$1,-\frac{1}{2},\frac{1}{3},-\frac{1}{4},\frac{1}{5},-\frac{1}{6},…$按一定规律排列如下：
第1行 1
第2行 $-\frac{1}{2}$ $\frac{1}{3}$
第3行 $-\frac{1}{4}$ $\frac{1}{5}$ $-\frac{1}{6}$
第4行 $\frac{1}{7}$ $-\frac{1}{8}$ $\frac{1}{9}$ $-\frac{1}{10}$
第5行 $\frac{1}{11}$ $-\frac{1}{12}$ $\frac{1}{13}$ $-\frac{1}{14}$ $\frac{1}{15}$
……
试确定第10行从左至右第8个数是什么？

答案： 【解析】：
首先，观察数列的排列规律，可以看到数列的每一行数字个数等于行号，且数列的分子始终为1，分母则是从1开始逐个递增的正整数。此外，数列的符号交替出现，即正负相间。
1.确定第10行之前的所有数字个数:
第1行有1个数，第2行有2个数，以此类推，第9行有9个数。
因此，前9行共有$1+2+3+...+9 = \frac{9 × (9 + 1)}{2} = 45$个数。
2.确定第10行的第1个数的分母:
由于前9行已经占据了45个位置，所以第10行的第1个数的分母是$45 + 1 = 46$。
3.确定第10行第8个数的分母和符号:
第10行的第8个数，其分母为$46 + 8 - 1 = 53$（因为第10行的第1个数的分母是46，所以第8个数的分母是46加上7再加1，即53）。
由于数列的符号是正负相间，且第10行的第一个数是正数（因为46是偶数，而数列的符号是交替的，所以偶数分母对应的数是负数，但行首的第一个数符号与行号加1的奇偶性相同，10加1为奇数，所以是正数），因此第8个数（偶数位置）的符号为负。
【答案】：
第10行从左至右第8个数是$-\frac{1}{53}$。