《2025年5年中考3年模拟七年级数学上册苏科版》

1.如图,现有底面直径为16cm,高为30cm的圆柱形容器,里面装满了果汁,小亮要把果汁分装到底面直径为8cm的10个小圆柱杯子里(每个杯子刚好装满),与好友分享,则杯子的高度为12cm.

答案： 答案　12
解析　设杯子的高度为x cm，
根据题意，得$10π×(\frac {8}{2})^{2}x=π(\frac {16}{2})^{2}×30$，解得$x = 12$。
所以杯子的高度是12 cm。

2.如图,将一个正方形先剪去一个宽为4的长方形,再剪去一个宽为5的长方形,且剪下来的两个长方形面积相等,则原正方形的面积为400.

答案： 答案　400
解析　设原正方形的边长为x。根据题意，得$4x = 5(x - 4)$，解得$x = 20$，$20×20 = 400$，故原正方形的面积为400。

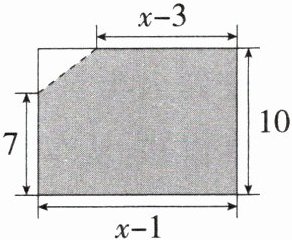
3.「2024江苏淮安期末」如图,将一张长方形纸片沿虚线剪去一个三角形,剩余部分(阴影部分)的面积为110,根据图中标注的长度求x的值.

答案： 解析　阴影部分的面积为$10(x - 1)-\frac {1}{2}×(10 - 7)[x - 1-(x - 3)] = 110$，整理，得$10x - 13 = 110$，解得$x = 12.3$。

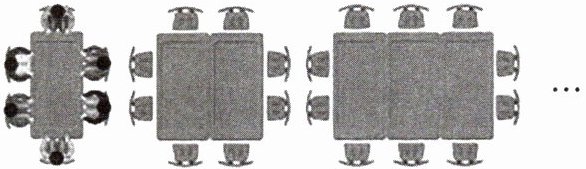
4.教材变式P136T21「2025江苏连云港海州期末」一张长方形桌子四周可坐6人,将一些相同的桌子按如图所示的方式拼在一起.若n张这样的长方形桌子拼在一起可以坐46人,则n= (A)

A.21
B.20
C.19
D.18

答案： A　因为1张桌子可坐$2×1 + 4 = 6$人，2张桌子拼在一起可坐$2×2 + 4 = 8$人，3张桌子拼在一起可坐$2×3 + 4 = 10$人，……，所以n张桌子拼在一起可坐$(4 + 2n)$人。
当$4 + 2n = 46$时，解得$n = 21$。故选A。

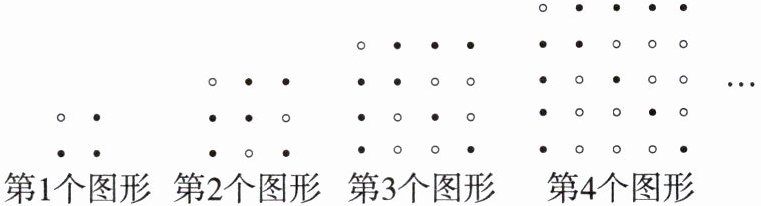
5.「2025江苏常州期末节选」我国著名数学家华罗庚先生说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休.”利用数形结合,可以从代数角度解决图形问题,也可以通过图形关系解决代数问题.用黑白两色棋子按如图所示的方式摆放.
(1)按此规律,第3个图形和第4个图形中黑色棋子的个数分别为9、12.
(2)按此规律,某个图形中的黑色棋子的个数可能是40吗?请说明理由.

不可能，理由如下：由所给图形可知，第1个图形中黑色棋子的个数为$3 = 3×1$；第2个图形中黑色棋子的个数为$6 = 3×2$；第3个图形中黑色棋子的个数为$9 = 3×3$；……所以第n个图形中黑色棋子的个数为3n。令$3n = 40$，解得$n = \frac{40}{3}$。因为n为正整数，所以某个图形中的黑色棋子的个数不可能是40。

答案： 解析　
(1)由题图可知，第3个图形中黑色棋子的个数为9，第4个图形中黑色棋子的个数为12。故答案为9；12。
(2)不可能，理由如下：
由所给图形可知，
第1个图形中黑色棋子的个数为$3 = 3×1$；
第2个图形中黑色棋子的个数为$6 = 3×2$；
第3个图形中黑色棋子的个数为$9 = 3×3$；
……
所以第n个图形中黑色棋子的个数为3n。
令$3n = 40$，解得$n = \frac{40}{3}$。
因为n为正整数，
所以某个图形中的黑色棋子的个数不可能是40。