第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
11.综合与实践:
【基础巩固】
(1)如图1,点E,B,F都在线段AC上,$AE= \frac {1}{2}EB$,F是BC的中点,则图中共有
【深入探究】
(2)在(1)的条件下,若$BF= \frac {1}{5}AC$,试探究EF与AC之间的数量关系,并说明理由.
【拓展提高】
(3)如图2,在(2)的基础上,G是AE的中点,若$AC= 20cm$,求GF的长.
【基础巩固】
(1)如图1,点E,B,F都在线段AC上,$AE= \frac {1}{2}EB$,F是BC的中点,则图中共有
10
条线段.【深入探究】
(2)在(1)的条件下,若$BF= \frac {1}{5}AC$,试探究EF与AC之间的数量关系,并说明理由.
5EF=3AC.理由如下:设BF=x.因为BF=$\frac{1}{5}$AC,所以AC=5BF=5x.因为F是BC的中点,所以BC=2BF=2x,所以AB=AC−BC=5x−2x=3x.因为AE=$\frac{1}{2}$EB,所以BE=$\frac{2}{3}$AB=2x,所以EF=BE+BF=2x+x=3x,所以5EF=3AC.
【拓展提高】
(3)如图2,在(2)的基础上,G是AE的中点,若$AC= 20cm$,求GF的长.
设BF=ycm,由(2)得AC=5ycm,EF=3ycm,AE=ycm,因为AC=20cm,所以5y=20,所以y=4,所以AE=4cm,EF=12cm.因为G是AE的中点,所以GE=$\frac{1}{2}$AE=2cm,所以GF=GE+EF=2+12=14(cm).
答案:
(1)10(2)5EF=3AC.理由如下:设BF=x.因为BF=$\frac{1}{5}$AC,所以AC=5BF=5x.因为F是BC的中点,所以BC=2BF=2x,所以AB=AC−BC=5x−2x=3x.因为AE=$\frac{1}{2}$EB,所以BE=$\frac{2}{3}$AB=2x,所以EF=BE+BF=2x+x=3x,所以5EF=3AC.(3)设BF=ycm,由(2)得AC=5ycm,EF=3ycm,AE=ycm,因为AC=20cm,所以5y=20,所以y=4,所以AE=4cm,EF=12cm.因为G是AE的中点,所以GE=$\frac{1}{2}$AE=2cm,所以GF=GE+EF=2+12=14(cm).
1.如图,D是线段AB上的一点,点C是AB的中点,$AB= 6,DB= 1$,则$CD= $ (
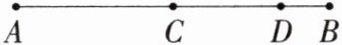
A.1
B.2
C.3
D.6
B
)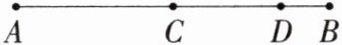
A.1
B.2
C.3
D.6
答案:
B
2.如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2 cm,那么AC比BC长
4cm
.
答案:
4cm
3.如图,已知线段$AB= 24cm$,C为AB延长线上一点,且$BC= \frac {1}{3}AB$.
(1)求AC的长.
(2)若D是AB的中点,E是AC的中点,求DE的长.
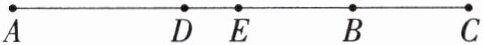
(1)求AC的长.
(2)若D是AB的中点,E是AC的中点,求DE的长.
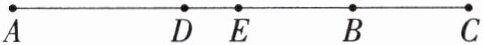
答案:
(1)因为BC=$\frac{1}{3}$AB,AB=24cm,所以BC=$\frac{1}{3}$×24=8(cm),所以AC=AB+BC=24+8=32(cm).(2)因为D是AB的中点,E是AC的中点,所以AD=$\frac{1}{2}$AB=12cm,AE=$\frac{1}{2}$AC=16cm,所以DE=AE−AD=16−12=4(cm).
查看更多完整答案,请扫码查看


