第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
10.「2025江苏无锡天一实验学校月考,★☆」将一张正方形纸片ABCD按如图所示的方式折叠,AE,AF为折痕,点B,D折叠后的对应点分别为$B',D'$,若$∠B'AD'= 26^{\circ }$,则$∠EAF$的度数为 (
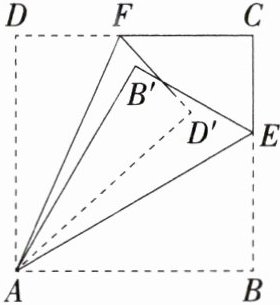
A.$51^{\circ }$
B.$45^{\circ }$
C.$40^{\circ }$
D.$32^{\circ }$
D
)
A.$51^{\circ }$
B.$45^{\circ }$
C.$40^{\circ }$
D.$32^{\circ }$
答案:
D 因为四边形ABCD为正方形,所以∠DAB = 90°,由折叠的性质可得∠BAE = ∠B'AE,∠DAF = ∠D'AF,所以2∠DAF + 2∠BAE = ∠DAB + ∠B'AD',因为∠B'AD' = 26°,所以2(∠DAF + ∠BAE) = 90° + 26° = 116°,所以∠DAF + ∠BAE = 58°,所以∠EAF = 90° - (∠DAF + ∠BAE) = 90° - 58° = 32°.故选D.
11.「2024江苏常州金坛期末,★☆」已知$∠AOB= 20^{\circ },∠AOC= 4∠AOB$,OD平分$∠AOB$,OM平分$∠AOC$,则$∠DOM$的度数是 ( )
A.$20^{\circ }或50^{\circ }$
B.$20^{\circ }或60^{\circ }$
C.$30^{\circ }或50^{\circ }$
D.$30^{\circ }或60^{\circ }$
A.$20^{\circ }或50^{\circ }$
B.$20^{\circ }或60^{\circ }$
C.$30^{\circ }或50^{\circ }$
D.$30^{\circ }或60^{\circ }$
答案:
C 分两种情况:
①如图1,当∠AOB的边OB在∠AOC内部时,因为∠AOB = 20°,∠AOC = 4∠AOB,所以∠AOC = 80°,因为OD平分∠AOB,OM平分∠AOC,所以∠AOD = $\frac{1}{2}$∠AOB = 10°,∠AOM = $\frac{1}{2}$∠AOC = 40°,所以∠DOM = ∠AOM - ∠AOD = 40° - 10° = 30°;

②如图2,当∠AOB的边OB在∠AOC外部时,易知∠DOM = ∠AOM + ∠AOD = 40° + 10° = 50°.

故选C.
C 分两种情况:
①如图1,当∠AOB的边OB在∠AOC内部时,因为∠AOB = 20°,∠AOC = 4∠AOB,所以∠AOC = 80°,因为OD平分∠AOB,OM平分∠AOC,所以∠AOD = $\frac{1}{2}$∠AOB = 10°,∠AOM = $\frac{1}{2}$∠AOC = 40°,所以∠DOM = ∠AOM - ∠AOD = 40° - 10° = 30°;

②如图2,当∠AOB的边OB在∠AOC外部时,易知∠DOM = ∠AOM + ∠AOD = 40° + 10° = 50°.

故选C.
12.「2024北京海淀首师大附中开学测试,★☆」如图,$∠AOB= α(0^{\circ }<α<60^{\circ }),∠COD= 2α$,OE为$∠AOC$的平分线,点B与点E在直线AO的两侧.
(1)当点A,O,C在一条直线上时,求$∠AOD和∠BOE$的大小(用含α的式子表示).
(2)在(1)的条件下,将$∠COD$绕点O顺时针旋转$180^{\circ }$,用等式表示旋转过程中$∠AOD与∠BOE$的数量关系.
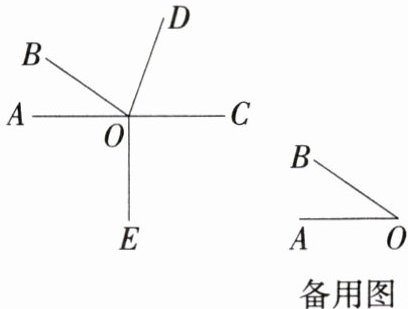
(1)当点A,O,C在一条直线上时,求$∠AOD和∠BOE$的大小(用含α的式子表示).
(2)在(1)的条件下,将$∠COD$绕点O顺时针旋转$180^{\circ }$,用等式表示旋转过程中$∠AOD与∠BOE$的数量关系.

答案:
解析
(1)∠AOD = 180° - ∠COD = 180° - 2α.因为OE为∠AOC的平分线,所以∠AOE = 90°,所以∠BOE = ∠AOB + ∠AOE = 90° + α.
(2)设旋转角为β,∠DOC旋转至∠D'OC'.当0°<β<60°时,∠DOD' = ∠COC' = β,如图1所示,所以∠COD' = ∠DOC - ∠DOD' = 2α - β,∠AOC' = 180° - ∠COC' = 180° - β,所以∠AOD' = 180° - ∠COD' = 180° - (2α - β),即2α - β = 180° - ∠AOD'.因为OE为∠AOC'的平分线,所以∠AOE = $\frac{180° - β}{2}$,所以∠BOE = ∠AOB + ∠AOE = α + $\frac{180° - β}{2}$,所以2∠BOE = 2α + 180° - β = 2α - β + 180°,所以2∠BOE = 180° - ∠AOD' + 180°,所以2∠BOE + ∠AOD' = 360°.

当60°<β<180°时,∠DOD' = ∠COC' = β,如图2所示,所以∠COD' = ∠DOD' - ∠COD = β - 2α,所以∠AOD' = 180° - ∠COD' = 180° - (β - 2α),即2α - β = ∠AOD' - 180°,所以∠AOC' = ∠AOD' - ∠C'OD' = 180° - (β - 2α) - 2α = 180° - β,因为OE为∠AOC'的平分线,所以∠AOE = $\frac{180° - β}{2}$,所以∠BOE = ∠AOB + ∠AOE = α + $\frac{180° - β}{2}$,所以2∠BOE = 2α + 180° - β = 2α - β + 180°,所以2∠BOE = ∠AOD' - 180° + 180°,所以2∠BOE = ∠AOD'.
综上所述,∠AOD与∠BOE的数量关系是2∠BOE + ∠AOD = 360°或2∠BOE = ∠AOD.
解析
(1)∠AOD = 180° - ∠COD = 180° - 2α.因为OE为∠AOC的平分线,所以∠AOE = 90°,所以∠BOE = ∠AOB + ∠AOE = 90° + α.
(2)设旋转角为β,∠DOC旋转至∠D'OC'.当0°<β<60°时,∠DOD' = ∠COC' = β,如图1所示,所以∠COD' = ∠DOC - ∠DOD' = 2α - β,∠AOC' = 180° - ∠COC' = 180° - β,所以∠AOD' = 180° - ∠COD' = 180° - (2α - β),即2α - β = 180° - ∠AOD'.因为OE为∠AOC'的平分线,所以∠AOE = $\frac{180° - β}{2}$,所以∠BOE = ∠AOB + ∠AOE = α + $\frac{180° - β}{2}$,所以2∠BOE = 2α + 180° - β = 2α - β + 180°,所以2∠BOE = 180° - ∠AOD' + 180°,所以2∠BOE + ∠AOD' = 360°.

当60°<β<180°时,∠DOD' = ∠COC' = β,如图2所示,所以∠COD' = ∠DOD' - ∠COD = β - 2α,所以∠AOD' = 180° - ∠COD' = 180° - (β - 2α),即2α - β = ∠AOD' - 180°,所以∠AOC' = ∠AOD' - ∠C'OD' = 180° - (β - 2α) - 2α = 180° - β,因为OE为∠AOC'的平分线,所以∠AOE = $\frac{180° - β}{2}$,所以∠BOE = ∠AOB + ∠AOE = α + $\frac{180° - β}{2}$,所以2∠BOE = 2α + 180° - β = 2α - β + 180°,所以2∠BOE = ∠AOD' - 180° + 180°,所以2∠BOE = ∠AOD'.
综上所述,∠AOD与∠BOE的数量关系是2∠BOE + ∠AOD = 360°或2∠BOE = ∠AOD.
13.我们可以把有公共顶点和一条公共边的两个角称为“共边角”.
(1)请写出图中的一组“共边角”.
(2)$∠AOB与∠BOC$是一组“共边角”,其中$∠AOB= 90^{\circ },∠BOC= 30^{\circ }$,请画出图形,并计算非公共边的两边所夹的角的度数.
(3)若一组“共边角”$∠AOB与∠BOC$非公共边的两边所夹的角是直角,请画出图形,这一组“共边角”的平分线所夹的角的度数确定吗?如果确定,请求出它的度数;如果不确定,请说明理由.
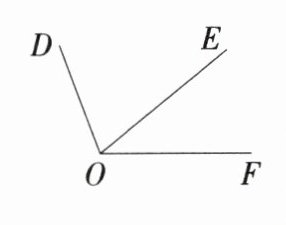
(1)请写出图中的一组“共边角”.
(2)$∠AOB与∠BOC$是一组“共边角”,其中$∠AOB= 90^{\circ },∠BOC= 30^{\circ }$,请画出图形,并计算非公共边的两边所夹的角的度数.
(3)若一组“共边角”$∠AOB与∠BOC$非公共边的两边所夹的角是直角,请画出图形,这一组“共边角”的平分线所夹的角的度数确定吗?如果确定,请求出它的度数;如果不确定,请说明理由.

答案:
解析
(1)题图中的“共边角”为∠DOE与∠DOF或∠DOE与∠EOF或∠DOF与∠EOF(写出一组即可).
(2)当OC在∠AOB内部时,如图1所示,∠AOC = ∠AOB - ∠BOC = 90° - 30° = 60°;

当OC在∠AOB外部时,如图2所示,∠AOC = ∠AOB + ∠BOC = 90° + 30° = 120°.
综上,非公共边的两边所夹的角的度数为60°或120°.
(3)这一组“共边角”的平分线所夹的角的度数确定,其度数为45°或135°.
如图1,当OB在∠AOC内部时,∠AOC = 90°,设OM,ON分别是∠AOB,∠BOC的平分线,所以∠BOM = $\frac{1}{2}$∠AOB,∠BON = $\frac{1}{2}$∠BOC,所以∠MON = ∠BOM + ∠BON = $\frac{1}{2}$(∠AOB + ∠BOC) = $\frac{1}{2}$∠AOC.因为∠AOC = 90°,所以∠MON = 45°.

如图2,当OB在∠AOC的外部时,∠AOC = 90°.设OM,ON分别是∠AOB,∠BOC的平分线,所以∠BOM = $\frac{1}{2}$∠AOB,∠BON = $\frac{1}{2}$∠BOC,所以∠MON = ∠BOM + ∠BON = $\frac{1}{2}$(∠AOB + ∠BOC).因为∠AOB + ∠BOC = 360° - ∠AOC = 270°,所以∠MON = $\frac{1}{2}$×270° = 135°.

综上,这一组“共边角”的平分线所夹的角的度数为45°或135°.
解析
(1)题图中的“共边角”为∠DOE与∠DOF或∠DOE与∠EOF或∠DOF与∠EOF(写出一组即可).
(2)当OC在∠AOB内部时,如图1所示,∠AOC = ∠AOB - ∠BOC = 90° - 30° = 60°;

当OC在∠AOB外部时,如图2所示,∠AOC = ∠AOB + ∠BOC = 90° + 30° = 120°.
综上,非公共边的两边所夹的角的度数为60°或120°.
(3)这一组“共边角”的平分线所夹的角的度数确定,其度数为45°或135°.
如图1,当OB在∠AOC内部时,∠AOC = 90°,设OM,ON分别是∠AOB,∠BOC的平分线,所以∠BOM = $\frac{1}{2}$∠AOB,∠BON = $\frac{1}{2}$∠BOC,所以∠MON = ∠BOM + ∠BON = $\frac{1}{2}$(∠AOB + ∠BOC) = $\frac{1}{2}$∠AOC.因为∠AOC = 90°,所以∠MON = 45°.

如图2,当OB在∠AOC的外部时,∠AOC = 90°.设OM,ON分别是∠AOB,∠BOC的平分线,所以∠BOM = $\frac{1}{2}$∠AOB,∠BON = $\frac{1}{2}$∠BOC,所以∠MON = ∠BOM + ∠BON = $\frac{1}{2}$(∠AOB + ∠BOC).因为∠AOB + ∠BOC = 360° - ∠AOC = 270°,所以∠MON = $\frac{1}{2}$×270° = 135°.

综上,这一组“共边角”的平分线所夹的角的度数为45°或135°.
查看更多完整答案,请扫码查看


