第88页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 已知一次函数的图象经过点$(1,1),(2,-4)$,则该一次函数的表达式为(
A. $y= 3x-2$
B. $y= -3x+4$
C. $y= -5x+6$
D. $y= 6x-5$
C
)A. $y= 3x-2$
B. $y= -3x+4$
C. $y= -5x+6$
D. $y= 6x-5$
答案:
C
2. 根据下表中一次函数的自变量$x与函数y$的对应值,可得$p$的值为(
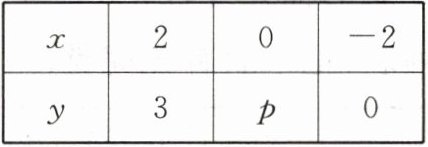
A. $\frac {3}{2}$
B. $-1$
C. $1$
D. $-\frac {3}{2}$
A
)
A. $\frac {3}{2}$
B. $-1$
C. $1$
D. $-\frac {3}{2}$
答案:
A
3. 已知$y是关于x$的一次函数,且当$x= 1$时,$y= -4$;当$x= 2$时,$y= -6$,则$y关于x$的函数表达式是
$ y = - 2x - 2 $
.
答案:
$ y = - 2x - 2 $
4. 如图,直线$y= \frac {1}{2}x+1与x轴交于点A$,点$A关于y轴的对称点为点A'$.设经过点$A'和y轴上的点B(0,2)的直线的表达式为y= kx+b$.
(1)求点$A'$的坐标.
(2)确定直线$A'B$的表达式.
(1)
(2)
(1)求点$A'$的坐标.
(2)确定直线$A'B$的表达式.
(1)
(2, 0)
(2)
y = - x + 2
答案:
解:
(1) 在 $ y = \frac { 1 } { 2 } x + 1 $ 中, 令 $ y = 0 $, 则 $ \frac { 1 } { 2 } x + 1 = 0 $, 解得 $ x = - 2 $. $ \therefore A ( - 2, 0 ) $. $ \because $ 点 $ A $ 关于 $ y $ 轴的对称点为点 $ A ^ { \prime } $, $ \therefore A ^ { \prime } ( 2, 0 ) $.
(2) $ \because A ^ { \prime } ( 2, 0 ) $, $ B ( 0, 2 ) $, $ \therefore \left\{ \begin{array} { l } { 2 k + b = 0 }, \\ { b = 2 }. \end{array} \right. $ 解得 $ \left\{ \begin{array} { l } { k = - 1 }, \\ { b = 2 }. \end{array} \right. $ $ \therefore $ 直线 $ A ^ { \prime } B $ 的表达式为 $ y = - x + 2 $.
(1) 在 $ y = \frac { 1 } { 2 } x + 1 $ 中, 令 $ y = 0 $, 则 $ \frac { 1 } { 2 } x + 1 = 0 $, 解得 $ x = - 2 $. $ \therefore A ( - 2, 0 ) $. $ \because $ 点 $ A $ 关于 $ y $ 轴的对称点为点 $ A ^ { \prime } $, $ \therefore A ^ { \prime } ( 2, 0 ) $.
(2) $ \because A ^ { \prime } ( 2, 0 ) $, $ B ( 0, 2 ) $, $ \therefore \left\{ \begin{array} { l } { 2 k + b = 0 }, \\ { b = 2 }. \end{array} \right. $ 解得 $ \left\{ \begin{array} { l } { k = - 1 }, \\ { b = 2 }. \end{array} \right. $ $ \therefore $ 直线 $ A ^ { \prime } B $ 的表达式为 $ y = - x + 2 $.
5. (2024·山西)生物学研究表明,某种蛇在一定生长阶段,其体长$y(cm)是尾长x(cm)$的一次函数,部分数据如下表所示,则$y与x$之间的关系式为(

A. $y= 7.5x+0.5$
B. $y= 7.5x-0.5$
C. $y= 15x$
D. $y= 15x+45.5$
A
)
A. $y= 7.5x+0.5$
B. $y= 7.5x-0.5$
C. $y= 15x$
D. $y= 15x+45.5$
答案:
A
6. 某品牌鞋子的长度$y(cm)$与鞋子的“码”数$x$之间满足一次函数关系.若$22码鞋子的长度为16 cm$,$44码鞋子的长度为27 cm$,则$38$码鞋子的长度为(
A. $23 cm$
B. $24 cm$
C. $25 cm$
D. $26 cm$
B
)A. $23 cm$
B. $24 cm$
C. $25 cm$
D. $26 cm$
答案:
B
7. 某种藤类植物四个阶段的平均长度$y(cm)与生长时间x$(天)的函数关系图象如图所示.当藤蔓长度大约在$115 cm$时,植物进入浆果生长期,此时植物的生长时间是(
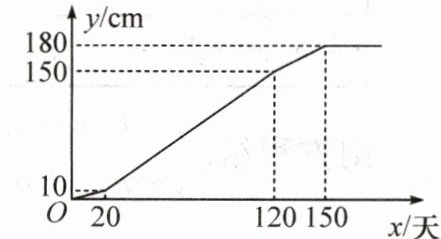
A. $90$天
B. $95$天
C. $140$天
D. $143$天
B
)
A. $90$天
B. $95$天
C. $140$天
D. $143$天
答案:
B
8. (教材P132新增习题T6变式)科学家探究出一定质量的某气体在体积不变的情况下,压强$p(kPa)是温度t(^{\circ }C)$的一次函数,其图象为如图所示的射线$AB$.
(1)根据图象求出上述气体的压强$p与温度t$的函数表达式.
(2)当压强为$200 kPa$时,求上述气体的温度.

(1)根据图象求出上述气体的压强$p与温度t$的函数表达式.
$ p = \frac { 2 } { 5 } t + 110 ( t \geq 0 ) $
(2)当压强为$200 kPa$时,求上述气体的温度.
$225 ^ { \circ } \mathrm { C }$

答案:
解:
(1) 设一次函数的表达式为 $ p = k t + b $. $ \because $ 函数的图象过点 $ ( 0, 110 ) $, $ ( 25, 120 ) $, $ \therefore \left\{ \begin{array} { l } { b = 110 }, \\ { 25 k + b = 120 }. \end{array} \right. $ 解得 $ \left\{ \begin{array} { l } { k = \frac { 2 } { 5 } }, \\ { b = 110 }. \end{array} \right. $ $ \therefore $ 所求的函数表达式是 $ p = \frac { 2 } { 5 } t + 110 ( t \geq 0 ) $.
(2) 当 $ p = 200 \mathrm { kPa } $ 时, 由
(1) 得, $ \frac { 2 } { 5 } t + 110 = 200 $, 解得 $ t = 225 $. $ \therefore $ 当压强为 $ 200 \mathrm { kPa } $ 时, 气体的温度是 $ 225 ^ { \circ } \mathrm { C } $.
(1) 设一次函数的表达式为 $ p = k t + b $. $ \because $ 函数的图象过点 $ ( 0, 110 ) $, $ ( 25, 120 ) $, $ \therefore \left\{ \begin{array} { l } { b = 110 }, \\ { 25 k + b = 120 }. \end{array} \right. $ 解得 $ \left\{ \begin{array} { l } { k = \frac { 2 } { 5 } }, \\ { b = 110 }. \end{array} \right. $ $ \therefore $ 所求的函数表达式是 $ p = \frac { 2 } { 5 } t + 110 ( t \geq 0 ) $.
(2) 当 $ p = 200 \mathrm { kPa } $ 时, 由
(1) 得, $ \frac { 2 } { 5 } t + 110 = 200 $, 解得 $ t = 225 $. $ \therefore $ 当压强为 $ 200 \mathrm { kPa } $ 时, 气体的温度是 $ 225 ^ { \circ } \mathrm { C } $.
查看更多完整答案,请扫码查看


