《2025年名校课堂八年级数学上册北师大版》

12. 比较下列各组数的大小,错误的是(B)
A. $\sqrt {8}＜\sqrt {10}$
B. $\frac {\sqrt {5}-1}{2}＜0.5$
C. $\frac {\sqrt {5}+1}{2}＞0.5$
D. $\sqrt {50}＞7$

答案： B

13. (2024·重庆)已知$m= \sqrt {27}-\sqrt {3}$,则实数m的取值范围是(B)
A. $2＜m＜3$
B. $3＜m＜4$
C. $4＜m＜5$
D. $5＜m＜6$

答案： B

14. 比较大小：$\frac {\sqrt {13}-2}{6}$＜$\frac {1}{3}$.(填“＞”“＜”或“=”)

答案： $＜$

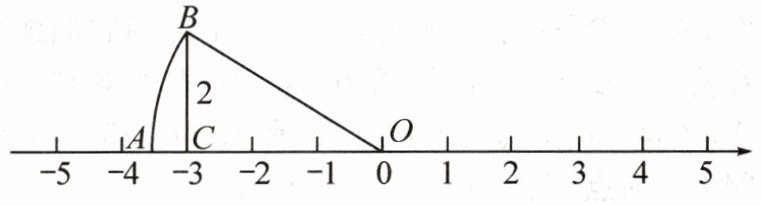
15. 如图所示,已知$OA= OB,BC= 2$.
(1)数轴上点A所表示的数为$-\sqrt{13}$.
(2)比较点A所表示的数与-3.5的大小：$-\sqrt{13}＜-3.5$.
(3)在数轴上找出$\sqrt {10}$对应的点.(不写作法保留作图痕迹)

(3) 图略, 点 $G$ 表示的数为 $\sqrt{10}$.

答案： 解:
(1) $-\sqrt{13}$
(2) $-\sqrt{13}＜-3.5$
(3) 图略, 点 $G$ 表示的数为 $\sqrt{10}$.

16. 下列计算正确的是(D)
A. $\sqrt {6}÷(\sqrt {3}-\sqrt {2})= \sqrt {2}-\sqrt {3}$
B. $2\sqrt {3}+3\sqrt {2}= 5\sqrt {5}$
C. $\sqrt {(π-3.14)^{2}}= 3.14-π$
D. $\sqrt {48}×\sqrt {3}= 12$

答案： D

17. 计算：
(1)$|\sqrt {7}-3|-2\sqrt {3}×\sqrt {21}$.
(2)$\sqrt {48}÷\sqrt {3}-\sqrt {\frac {1}{2}}×2\sqrt {3}+\sqrt {24}$.
(3)$(3\sqrt {2}+2\sqrt {3})(3\sqrt {2}-2\sqrt {3})-(\sqrt {5}-\sqrt {3})^{2}$.

答案： 解:
(1) 原式 $=3-\sqrt{7}-2 \times 3 \sqrt{7}=3-\sqrt{7}-6 \sqrt{7}=3-7 \sqrt{7}$.
(2) 原式 $=\sqrt{16}-\frac{\sqrt{2}}{2} \times 2 \sqrt{3}+2 \sqrt{6}=4-\sqrt{6}+2 \sqrt{6}=4+\sqrt{6}$.
(3) 原式 $=18-12-(5-2 \sqrt{15}+3)=18-12-8+2 \sqrt{15}=-2+2 \sqrt{15}$.

18. 阅读下列材料,然后解答问题.
在进行代数式化简时,我们有时会碰上如$\frac {5}{\sqrt {3}},\frac {2}{\sqrt {3}+1}$这样的式子,其实我们还可以将其进一步化简：
①$\frac {5}{\sqrt {3}}= \frac {5×\sqrt {3}}{\sqrt {3}×\sqrt {3}}= \frac {5}{3}\sqrt {3}$；
②$\frac {2}{\sqrt {3}+1}= \frac {2×(\sqrt {3}-1)}{(\sqrt {3}+1)(\sqrt {3}-1)}= \frac {2×(\sqrt {3}-1)}{(\sqrt {3})^{2}-1}= \sqrt {3}-1$.
这种化简的方法叫分母有理化.
(1)参照①式化简：$\frac {3}{\sqrt {5}}=$$\frac{3\sqrt{5}}{5}$.
(2)参照②式化简：$\frac {2}{\sqrt {5}+\sqrt {3}}=$$\sqrt{5}-\sqrt{3}$.
(3)化简：$\frac {1}{\sqrt {3}+1}+\frac {1}{\sqrt {5}+\sqrt {3}}+\frac {1}{\sqrt {7}+\sqrt {5}}+... +\frac {1}{\sqrt {99}+\sqrt {97}}$.
解: 原式 $=\frac{\sqrt{3}-1}{(\sqrt{3}+1)(\sqrt{3}-1)}+\frac{\sqrt{5}-\sqrt{3}}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}+\frac{\sqrt{7}-\sqrt{5}}{(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})}+\cdots+\frac{\sqrt{99}-\sqrt{97}}{(\sqrt{99}+\sqrt{97})(\sqrt{99}-\sqrt{97})}=\frac{\sqrt{3}-1}{2}+\frac{\sqrt{5}-\sqrt{3}}{2}+\frac{\sqrt{7}-\sqrt{5}}{2}+\cdots+\frac{\sqrt{99}-\sqrt{97}}{2}=\frac{1}{2} ×(\sqrt{3}-1+\sqrt{5}-\sqrt{3}+\sqrt{7}-\sqrt{5}+\cdots+\sqrt{99}-\sqrt{97})=\frac{\sqrt{99}-1}{2}=\frac{3 \sqrt{11}-1}{2}$.

答案： 解:
(1) $\frac{3 \sqrt{5}}{5}$
(2) $\sqrt{5}-\sqrt{3}$
(3) 原式 $=\frac{\sqrt{3}-1}{(\sqrt{3}+1)(\sqrt{3}-1)}+\frac{\sqrt{5}-\sqrt{3}}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}+\frac{\sqrt{7}-\sqrt{5}}{(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})}+\cdots+\frac{\sqrt{99}-\sqrt{97}}{(\sqrt{99}+\sqrt{97})(\sqrt{99}-\sqrt{97})}=\frac{\sqrt{3}-1}{2}+\frac{\sqrt{5}-\sqrt{3}}{2}+\frac{\sqrt{7}-\sqrt{5}}{2}+\cdots+\frac{\sqrt{99}-\sqrt{97}}{2}=\frac{1}{2} \times(\sqrt{3}-1+\sqrt{5}-\sqrt{3}+\sqrt{7}-\sqrt{5}+\cdots+\sqrt{99}-\sqrt{97})=\frac{\sqrt{99}-1}{2}=\frac{3 \sqrt{11}-1}{2}$.