第6页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 下列四组数能作为直角三角形的三边长的是(
A. 1,1,2
B. 6,7,8
C. 5,12,14
D. 3,4,5
D
)A. 1,1,2
B. 6,7,8
C. 5,12,14
D. 3,4,5
答案:
D
2. 在$\triangle ABC$中,$∠A,∠B,∠C的对边分别为a$, $b,c$,且$a^{2}-b^{2}= c^{2}$,则下列说法正确的是(
A. $∠C$是直角
B. $∠B$是直角
C. $∠A$是直角
D. $∠A$是锐角
C
)A. $∠C$是直角
B. $∠B$是直角
C. $∠A$是直角
D. $∠A$是锐角
答案:
C
3. 若$\triangle ABC的三边长a,b,c满足|a-7|+$ $|24-b|+(c-25)^{2}= 0$,则$\triangle ABC$是(
A. 直角三角形
B. 等腰三角形
C. 等边三角形
D. 等腰直角三角形
A
)A. 直角三角形
B. 等腰三角形
C. 等边三角形
D. 等腰直角三角形
答案:
A
4. 放学后,彬彬先去同学晓华家写了一个小时 的作业,然后才回到家里.已知学校$A$、晓华家 $B$、彬彬家$C$的两两之间的距离如图所示,且 晓华家$B在学校A$的正东方向,则彬彬家$C$ 在学校$A$的(
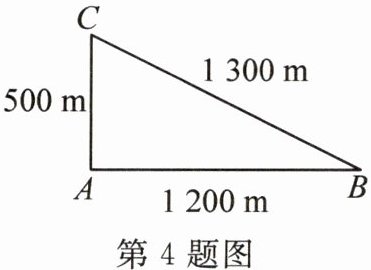
A. 正南方向
B. 正东方向
C. 正西方向
D. 正北方向
D
)
A. 正南方向
B. 正东方向
C. 正西方向
D. 正北方向
答案:
D
5. 如图,三个正方形的面积分别为$S_{1}= 3,S_{2}= 2,S_{3}= 1$,则分别以它们的一边为边围成的三角形中,$∠1+∠2= $
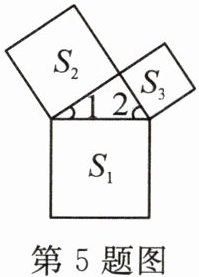
90
$^{\circ }$.
答案:
90
6. 木工做一个长方形桌面,量得桌面的长为 $2.4m$,宽为$1.8m$,对角线长为$3m$,则这个 桌面
合格
(填“合格”或“不合格”).
答案:
合格
7. 若一个三角形的三边长分别为$12,16,20$,则 它的面积为
96
.
答案:
96
8. 在$\triangle ABC$中,$∠A,∠B,∠C的对边分别为a$, $b,c$,已知$a= 2,b= \frac {5}{2},c= \frac {3}{2}$,则$\triangle ABC$是直角三角形吗?
小亮的解答如下:
解:$\triangle ABC$不是直角三角形.理由如下:
$\because a^{2}= 4,b^{2}+c^{2}= (\frac {5}{2})^{2}+(\frac {3}{2})^{2}= \frac {17}{2},$
$\therefore a^{2}≠b^{2}+c^{2}.$
$\therefore \triangle ABC$不是直角三角形.
请问小亮的解答正确吗?若不正确,请给出 正确的解答过程.
小亮的解答如下:
解:$\triangle ABC$不是直角三角形.理由如下:
$\because a^{2}= 4,b^{2}+c^{2}= (\frac {5}{2})^{2}+(\frac {3}{2})^{2}= \frac {17}{2},$
$\therefore a^{2}≠b^{2}+c^{2}.$
$\therefore \triangle ABC$不是直角三角形.
请问小亮的解答正确吗?若不正确,请给出 正确的解答过程.
解:小亮的解答不正确。正确的解答过程如下:$\triangle ABC$是直角三角形。理由如下:$\because a^{2}+c^{2}=2^{2}+(\frac{3}{2})^{2}=4+\frac{9}{4}=\frac{25}{4}$,$b^{2}=(\frac{5}{2})^{2}=\frac{25}{4}$,$\therefore a^{2}+c^{2}=b^{2}$。$\therefore \angle B=90^{\circ}$。$\therefore \triangle ABC$是直角三角形。
答案:
解:小亮的解答不正确。正确的解答过程如下:$\triangle ABC$是直角三角形。理由如下:$\because a^{2}+c^{2}=2^{2}+(\frac{3}{2})^{2}=4+\frac{9}{4}=\frac{25}{4}$,$b^{2}=(\frac{5}{2})^{2}=\frac{25}{4}$,$\therefore a^{2}+c^{2}=b^{2}$。$\therefore \angle B=90^{\circ}$。$\therefore \triangle ABC$是直角三角形。
9. 如图,在$\triangle ABC$中,$AD⊥BC$,垂足为$D$.如果 $AD= 6,BD= 9,CD= 4$,那么$∠BAC$是直角 吗?为什么?
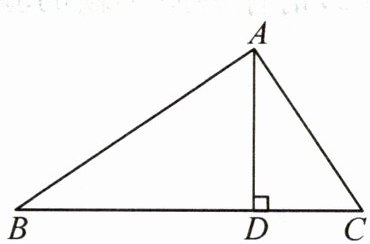
解:$∠BAC$是

解:$∠BAC$是
直角
。理由如下:$\because AD \perp BC$,$\therefore \angle ADB=\angle ADC=90^{\circ}$。$\therefore AD^{2}+BD^{2}=AB^{2}$,$AD^{2}+CD^{2}=AC^{2}$。$\because AD=6$,$BD=9$,$CD=4$,$\therefore AB^{2}=6^{2}+9^{2}=$117
,$AC^{2}=6^{2}+4^{2}=$52
。$\because BC=BD+CD=$13
,$\therefore BC^{2}=$169
。$\therefore AB^{2}+AC^{2}=BC^{2}$。$\therefore \angle BAC=$90°
。
答案:
解:$\angle BAC$是直角。理由如下:$\because AD \perp BC$,$\therefore \angle ADB=\angle ADC=90^{\circ}$。$\therefore AD^{2}+BD^{2}=AB^{2}$,$AD^{2}+CD^{2}=AC^{2}$。$\because AD=6$,$BD=9$,$CD=4$,$\therefore AB^{2}=6^{2}+9^{2}=117$,$AC^{2}=6^{2}+4^{2}=52$。$\because BC=BD+CD=13$,$\therefore BC^{2}=169$。$\therefore AB^{2}+AC^{2}=BC^{2}$。$\therefore \angle BAC=90^{\circ}$。
10. 下列给出的四组数中,是勾股数的一组是(
A. 1,2,3
B. 2,3,4
C. 0.3,0.4,0.5
D. 6,8,10
D
)A. 1,2,3
B. 2,3,4
C. 0.3,0.4,0.5
D. 6,8,10
答案:
D
11. 若$8,a,17$是一组勾股数,则$a= $
15
.
答案:
15
查看更多完整答案,请扫码查看


