第47页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
10. 在平面直角坐标系中,点$A(2,-3)与点B(2,3)$关于
x
轴对称.
答案:
x
11. 新考向 跨学科如图,这是蜡烛的平面镜成像的原理图,以桌面为x轴,镜面侧面为y轴(镜面厚度忽略不计)建立平面直角坐标系.如果某刻火焰顶尖点S的坐标是$(-4,2)$,那么此时对应的虚像顶尖点$S'$的坐标是
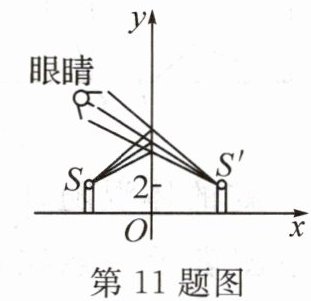
$(4,2)$
.
答案:
$(4,2)$
12. 在平面直角坐标系中,点P的坐标为$(a,2)$,其关于x轴对称的点Q的坐标为$(3,b)$,则$a+b$的值为 (
A. -1
B. 1
C. -5
D. 5
B
)A. -1
B. 1
C. -5
D. 5
答案:
B
13. 如图,在平面直角坐标系xOy中,$∠A= 90^{\circ },OA= 4$,OB平分$∠AO{x}$,点$B(a-1,a-2)$关于x轴的对称点是 (
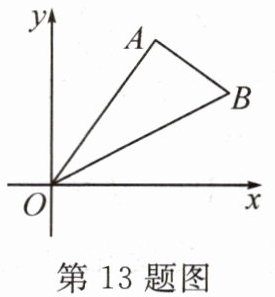
A. $(-4,3)$
B. $(5,-2)$
C. $(4,-3)$
D. $(5,-3)$
C
)
A. $(-4,3)$
B. $(5,-2)$
C. $(4,-3)$
D. $(5,-3)$
答案:
C
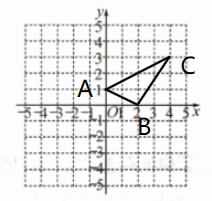
14. 如图所示,在平面直角坐标系中,已知$A(0,1),B(2,0),C(4,3)$.
(1)在平面直角坐标系中画出$△ABC$,则$△ABC$的面积是
(2)若点D与点C关于y轴对称,则点D的坐标为
(3)已知P为x轴上一点,若$△ABP$的面积为4,求点P的坐标.

(1)在平面直角坐标系中画出$△ABC$,则$△ABC$的面积是
4
.(2)若点D与点C关于y轴对称,则点D的坐标为
$(-4,3)$
.(3)已知P为x轴上一点,若$△ABP$的面积为4,求点P的坐标.

解: $\because S_{\triangle ABP} = \frac{1}{2}BP \cdot OA = 4$, $\therefore \frac{1}{2}BP×1 = 4$, 解得 $BP = 8$. ∴ 点 P 的横坐标为 $2 + 8 = 10$ 或 $2 - 8 = -6$. ∴ 点 P 的坐标为 $(10,0)$ 或 $(-6,0)$
答案:
解:
(1) 4
(2) $(-4,3)$
(3) $\because S_{\triangle ABP} = \frac{1}{2}BP \cdot OA = 4$, $\therefore \frac{1}{2}BP×1 = 4$, 解得 $BP = 8$.
∴ 点 P 的横坐标为 $2 + 8 = 10$ 或 $2 - 8 = -6$.
∴ 点 P 的坐标为 $(10,0)$ 或 $(-6,0)$.
解:
(1) 4

(2) $(-4,3)$
(3) $\because S_{\triangle ABP} = \frac{1}{2}BP \cdot OA = 4$, $\therefore \frac{1}{2}BP×1 = 4$, 解得 $BP = 8$.
∴ 点 P 的横坐标为 $2 + 8 = 10$ 或 $2 - 8 = -6$.
∴ 点 P 的坐标为 $(10,0)$ 或 $(-6,0)$.
15. 新考向 综合与实践问题情境:
在平面直角坐标系xOy中有不重合的两点$A(x_{1},y_{1})和B(x_{2},y_{2})$,小明在学习中发现,若$x_{1}= x_{2}$,则$AB// y$轴,且线段AB的长为$|y_{1}-y_{2}|$;若$y_{1}= y_{2}$,则$AB// x$轴,且线段AB的长为$|x_{1}-x_{2}|$.
【应用】
(1)若点$A(-1,1),B(2,1)$,则$AB// x$轴,AB的长为
(2)若点$C(1,0),CD// y$轴,且$CD= 2$,则点D的坐标为
【拓展】
我们规定:平面直角坐标系中任意不重合的两点$M(x_{1},y_{1}),N(x_{2},y_{2})之间的折线距离为d(M,N)= |x_{1}-x_{2}|+|y_{1}-y_{2}|$.例如:图1中,点$M(-1,1)与点N(1,-2)之间的折线距离为d(M,N)= |-1-1|+|1-(-2)|= 2+3= 5$.
解决下列问题:
(1)如图2,已知点$E(2,0)$,若$F(-1,-2)$,则$d(E,F)= $
(2)如图2,已知点$E(2,0),H(1,t)$,若$d(E,H)= 3$,则$t= $
(3)如图3,已知点$P(3,3)$,若点Q在x轴上,且$△OPQ$的面积为3,则$d(P,Q)= $

在平面直角坐标系xOy中有不重合的两点$A(x_{1},y_{1})和B(x_{2},y_{2})$,小明在学习中发现,若$x_{1}= x_{2}$,则$AB// y$轴,且线段AB的长为$|y_{1}-y_{2}|$;若$y_{1}= y_{2}$,则$AB// x$轴,且线段AB的长为$|x_{1}-x_{2}|$.
【应用】
(1)若点$A(-1,1),B(2,1)$,则$AB// x$轴,AB的长为
3
.(2)若点$C(1,0),CD// y$轴,且$CD= 2$,则点D的坐标为
$(1,2)$ 或 $(1,-2)$
.【拓展】
我们规定:平面直角坐标系中任意不重合的两点$M(x_{1},y_{1}),N(x_{2},y_{2})之间的折线距离为d(M,N)= |x_{1}-x_{2}|+|y_{1}-y_{2}|$.例如:图1中,点$M(-1,1)与点N(1,-2)之间的折线距离为d(M,N)= |-1-1|+|1-(-2)|= 2+3= 5$.
解决下列问题:
(1)如图2,已知点$E(2,0)$,若$F(-1,-2)$,则$d(E,F)= $
5
.(2)如图2,已知点$E(2,0),H(1,t)$,若$d(E,H)= 3$,则$t= $
2 或 -2
.(3)如图3,已知点$P(3,3)$,若点Q在x轴上,且$△OPQ$的面积为3,则$d(P,Q)= $
4 或 8
.
答案:
【应用】
(1) 3
(2) $(1,2)$ 或 $(1,-2)$ 【拓展】
(1) 5
(2) 2 或 -2
(3) 4 或 8
(1) 3
(2) $(1,2)$ 或 $(1,-2)$ 【拓展】
(1) 5
(2) 2 或 -2
(3) 4 或 8
查看更多完整答案,请扫码查看


