第4页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 用4个如图1所示的形状、大小完全一样的直角三角形拼一拼、摆一摆,可以摆成如图2所示的正方形,下面我们利用这个图形验证勾股定理.
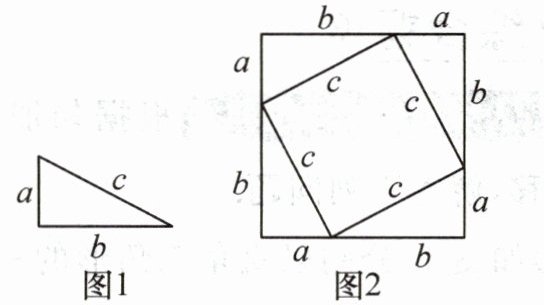
(1)图2中大正方形的边长为
(2)大正方形面积可以表示为
(3)对比这两种表示方法,可得出

(1)图2中大正方形的边长为
$a + b$
,里面小正方形的边长为$c$
.(2)大正方形面积可以表示为
$(a + b)^2$
,也可以表示为$4 × \frac{1}{2}ab + c^2$
.(3)对比这两种表示方法,可得出
$(a + b)^2 = 4 × \frac{1}{2}ab + c^2$
,整理,得$c^2 = a^2 + b^2$
.
答案:
(1) $ a + b $ $ c $
(2) $ (a + b)^2 $ $ 4 \times \frac{1}{2}ab + c^2 $
(3) $ (a + b)^2 = 4 \times \frac{1}{2}ab + c^2 $ $ c^2 = a^2 + b^2 $
(1) $ a + b $ $ c $
(2) $ (a + b)^2 $ $ 4 \times \frac{1}{2}ab + c^2 $
(3) $ (a + b)^2 = 4 \times \frac{1}{2}ab + c^2 $ $ c^2 = a^2 + b^2 $
2. (教材P8习题T3变式)如图,一棵高为8m的大树被台风刮断.若树在离地面3m的点C处折断,则树顶端落在离树底部(
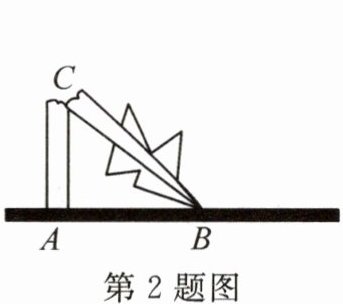
A. 4m处
B. 5m处
C. 6m处
D. 7m处
A
)
A. 4m处
B. 5m处
C. 6m处
D. 7m处
答案:
A
3. 一个外轮廓为长方形的机器零件平面示意图如图所示,根据图中标出的尺寸(单位:mm),可得出两圆孔中心A,B之间的距离为
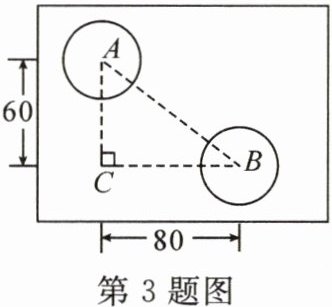
100
mm.
答案:
100
4. 新考向 真实情境(教材P6随堂练习T1变式)如图,AC⊥BC,原计划从A地经C地到B地修建一条无隧道高速公路,后因技术攻关,可以打通由A地到B地的隧道修建高速公路,其中隧道部分总长为2km.已知高速公路每千米造价为3000万元,隧道高速公路每千米造价为5000万元,AC= 80km,BC= 60km,则改建后可节省的工程费用是
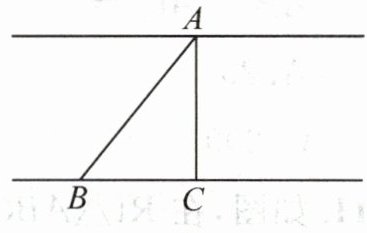
116000
万元.
答案:
解: 在 $ Rt\triangle ABC $ 中, $ AB^2 = BC^2 + AC^2 $, $ \therefore AB^2 = AC^2 + BC^2 = 80^2 + 60^2 = 10000 $. $ \therefore AB = 100 km $. $ (80 + 60) \times 3000 - (100 - 2) \times 3000 - 2 \times 5000 = 116000 $ (万元). 答: 改建后可节省的工程费用是 116000 万元.
5. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米.若保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A'D为1.5米,则小巷的宽为(
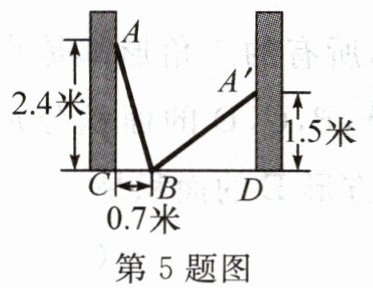
A. 2.5米
B. 2.6米
C. 2.7米
D. 2.8米
C
)
A. 2.5米
B. 2.6米
C. 2.7米
D. 2.8米
答案:
C
6. (2024·眉山)图1是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,由四个全等的直角三角形拼成.若图1中大正方形的面积为24,小正方形的面积为4,现将这四个直角三角形拼成图2,则图2中大正方形的面积为(
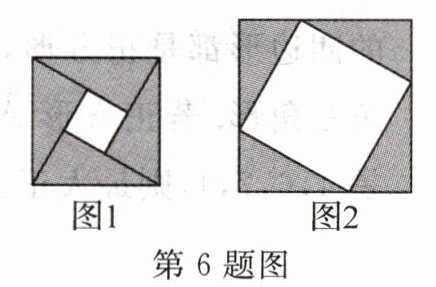
A. 24
B. 36
C. 40
D. 44
D
)
A. 24
B. 36
C. 40
D. 44
答案:
D
7. (教材P9习题T7变式)如图,某隧道的截面是一个半径为5.2m的半圆形,以中间线为界分成两条车道,试问一辆高4.1m、宽3m的卡车在一条车道内行驶能通过该隧道吗?(中间线宽忽略不计)
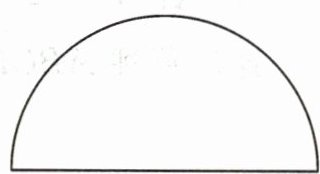
解: 过圆上一点 $ A $ 作地面的垂线, 垂足为 $ B $ (不与点 $ O $ 重合). 当 $ BO = 3m $ 时, $ AB^2 = AO^2 - OB^2 = 5.2^2 - 3^2 = 18.04 $, $ \because 4.1^2 = 16.81 < 18.04 $, $ \therefore $ 一辆高 $ 4.1m $、宽 $ 3m $ 的卡车在一条车道内行驶

解: 过圆上一点 $ A $ 作地面的垂线, 垂足为 $ B $ (不与点 $ O $ 重合). 当 $ BO = 3m $ 时, $ AB^2 = AO^2 - OB^2 = 5.2^2 - 3^2 = 18.04 $, $ \because 4.1^2 = 16.81 < 18.04 $, $ \therefore $ 一辆高 $ 4.1m $、宽 $ 3m $ 的卡车在一条车道内行驶
能
通过该隧道.
答案:
解: 过圆上一点 $ A $ 作地面的垂线, 垂足为 $ B $ (不与点 $ O $ 重合). 当 $ BO = 3m $ 时, $ AB^2 = AO^2 - OB^2 = 5.2^2 - 3^2 = 18.04 $, $ \because 4.1^2 = 16.81 < 18.04 $, $ \therefore $ 一辆高 $ 4.1m $、宽 $ 3m $ 的卡车在一条车道内行驶能通过该隧道.
查看更多完整答案,请扫码查看


