《2025年名校课堂八年级数学上册北师大版》

6. 大自然中的音乐与数学有着奇妙的联系,蟋蟀鸣叫就是其中的一种. 据悉在一定温度范围内,蟋蟀鸣叫的次数与气温关系密切,项目化学习小组统计了本地不同气温下某种蟋蟀每分钟鸣叫的次数,汇总如下表：

若这种蟋蟀每分钟鸣叫次数为 112 次,则该地当时的气温约为19 $ ^{\circ}C $.

答案： 19

7. 人大附中校本经典题 一个水库的水位在最近 $ 5h $ 内持续上涨. 下表记录了这 $ 5h $ 内 6 个时间点的水位高度,其中 $ t $ 表示时间,$ y $ 表示水位高度.

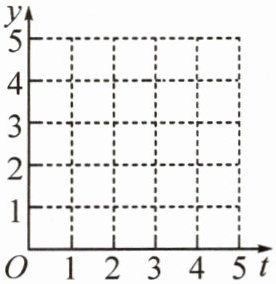
(1) 在平面直角坐标系中描出表中数据对应的点,由此你能发现水位变化有什么规律吗？这些点在同一条直线上，每经过1h，水位上涨0.3m
(2) 据估计这种上涨规律还会持续 $ 2h $,预测再过 $ 2h $ 水位高度将达到5.1米.
(3) 试写出水位高度 $ y $ 与时间 $ t $ 之间的关系式.$ y = 0.3t + 3 $

答案： 解:
(1) 在平面直角坐标系中描出表中数据对应的点, 图略. 由此可知, 这些点在同一条直线上. 水位变化的规律: 每经过 1 h, 水位上涨 0.3 m.
(2) 若这种上涨规律还会持续 2 h, 则 $ t = 7 $, 当 $ t = 7 $ 时, $ y = 0.3 \times 7 + 3 = 5.1 $,
∴ 再过 2 h 水位高度将达到 5.1 m.
(3) 水位高度 $ y $ 与时间 $ t $ 之间的关系式为 $ y = 0.3t + 3 $.

8. 石家庄外国语校本经典题 阅读理解：设 $ y $ 是 $ x $ 的函数,$ x_{1},x_{2} $ 是自变量 $ x $ 的取值范围内的两个值,当 $ x $ 由 $ x_{1} $ 变化到 $ x_{2} $ 时,对应的 $ y $ 值由 $ y_{1} $ 变化到 $ y_{2} $,我们称比值 $ \frac{y_{2} - y_{1}}{x_{2} - x_{1}} $ 为 $ y $ 在 $ x_{1} $ 与 $ x_{2} $ 之间的平均变化速度. 某兴趣小组调查了解到某型号汽车紧急刹车后车速每秒减少 $ a(m/s) $,该型号汽车刹车前初始速度为 $ v_{0}(m/s) $,刹车后速度 $ v(m/s) $ 与时间 $ t(s) $ 之间的关系如下表：

(1) 该汽车刹车前初始速度 $ v_{0} = $20 $ m/s $,求刹车时的平均变化速度.
(2) 写出刹车后速度 $ v $ 与时间 $ t $ 的关系式.
(1) 由题意可知, 刹车时的平均变化速度为 $ \frac{10 - 15}{2 - 1} = -5 (m/s) $. (2) $ v = 20 - 5t $

答案： 解:
(1) 20 由题意可知, 刹车时的平均变化速度为 $ \frac{10 - 15}{2 - 1} = -5 (m/s) $.
(2) $ v = 20 - 5t $.