《2025年名校课堂八年级数学上册北师大版》

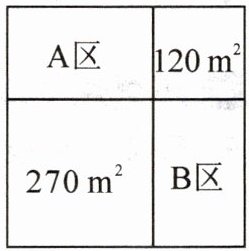
14. A|湖南师大附中校本经典题 某小区内有一块正方形空地,物业计划利用这块空地修建居民休闲区.具体规划如图所示,其中A区和B区为活动区域,剩余两个正方形区域为绿化区域,面积分别是$270 \mathrm { m } ^ { 2 }和120 \mathrm { m } ^ { 2 }$,则A区和B区的总面积为360$\mathrm { m } ^ { 2 }$.

答案： 360

15. 计算：
(1)$\sqrt { 2 } × ( \sqrt { 32 } - \frac { 1 } { \sqrt { 2 } } ) - \frac { \sqrt { 27 } + \sqrt { 12 } } { \sqrt { 3 } }$.
(2)$( \sqrt { 5 } - \sqrt { 2 } ) ( \sqrt { 5 } + \sqrt { 2 } ) - ( \sqrt { 5 } - 1 ) ^ { 2 }$.

答案： 解：
(1) 原式 $= \sqrt{64} - 1 - (\sqrt{9} + \sqrt{4}) = 8 - 1 - (3 + 2) = 7 - 5 = 2$。
(2) 原式 $= 5 - 2 - (5 - 2\sqrt{5} + 1) = 5 - 2 - 6 + 2\sqrt{5} = 2\sqrt{5} - 3$。

16. 新考向 阅读理解 阅读材料：
像$( \sqrt { 5 } + 2 ) ( \sqrt { 5 } - 2 ) = 1$,$\sqrt { a } \cdot \sqrt { a } = a ( a \geq 0 )$这种两个含二次根式的代数式相乘,积不含二次根式,我们称这两个代数式互为有理化因式.在进行二次根式的运算时,利用有理化因式可以化去分母中的根号.数学课上,老师出了一道题：“已知$a = \frac { 1 } { \sqrt { 2 } - 1 }$,求$3 a ^ { 2 } - 6 a - 1$的值.”
聪明的小明同学根据上述材料,作了这样的解答：
$\because a = \frac { 1 } { \sqrt { 2 } - 1 } = \frac { \sqrt { 2 } + 1 } { ( \sqrt { 2 } - 1 ) ( \sqrt { 2 } + 1 ) } = \sqrt { 2 } + 1$,
$\therefore a - 1 = \sqrt { 2 }$.$\therefore ( a - 1 ) ^ { 2 } = 2$.
$\therefore a ^ { 2 } - 2 a + 1 = 2$,即$a ^ { 2 } - 2 a = 1$.
$\therefore 3 a ^ { 2 } - 6 a = 3$.
$\therefore 3 a ^ { 2 } - 6 a - 1 = 3 - 1 = 2$.
请根据小明的解答过程,解决下列问题：
(1)化简：$\frac { 1 } { \sqrt { 10 } - 3 } = $$\sqrt{10} + 3$.
(2)若$a = \frac { 1 } { 3 + 2 \sqrt { 2 } }$,求$2 a ^ { 2 } - 12 a - 1$的值.
解：$\because a = \frac{1}{3 + 2\sqrt{2}} = \frac{3 - 2\sqrt{2}}{(3 + 2\sqrt{2})(3 - 2\sqrt{2})} = 3 - 2\sqrt{2}$，$\therefore a - 3 = -2\sqrt{2}$。$\therefore (a - 3)^2 = 8$。$\therefore a^2 - 6a + 9 = 8$，即 $a^2 - 6a = -1$。$\therefore 2a^2 - 12a = -2$。$\therefore 2a^2 - 12a - 1 = -2 - 1 = -3$。

答案： 解：
(1) $\sqrt{10} + 3$
(2) $\because a = \frac{1}{3 + 2\sqrt{2}} = \frac{3 - 2\sqrt{2}}{(3 + 2\sqrt{2})(3 - 2\sqrt{2})} = 3 - 2\sqrt{2}$，$\therefore a - 3 = -2\sqrt{2}$。$\therefore (a - 3)^2 = 8$。$\therefore a^2 - 6a + 9 = 8$，即 $a^2 - 6a = -1$。$\therefore 2a^2 - 12a = -2$。$\therefore 2a^2 - 12a - 1 = -2 - 1 = -3$。

1. (2024·甘南州)已知$x$,$y$为实数,若满足$y = \sqrt { x - 3 } + \sqrt { 3 - x } + 2$,则$x ^ { y }$的值为(D)
A. 5
B. 6
C. 8
D. 9

答案： D

2. 已知$a满足| 2024 - a | + \sqrt { a - 2025 } = a$,则$a - 2024 ^ { 2 }$的值为2025.

答案： 2025

3. (2024·成都)若$m$,$n$为实数,且$( m + 4 ) ^ { 2 } + \sqrt { n - 5 } = 0$,则$( m + n ) ^ { 2 }$的值为1.

答案： 1

4. 代数式$3 - \sqrt { 4 - x ^ { 2 } }$的最大值是3.

答案： 3

5. 若$a + \sqrt { a - 2 } = 2$,求$\sqrt { a + 2 }$的值.

答案： 解：$\because a + \sqrt{a - 2} = 2$，$\therefore \sqrt{a - 2} = 2 - a$。$\because a - 2 \geq 0$，$2 - a \geq 0$，$\therefore a = 2$。$\therefore \sqrt{a + 2} = \sqrt{4} = 2$。