第63页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 某物体在力F的作用下,沿力的方向移动的距离为s,力对物体所做的功W与s的对应关系如图所示,则下列结论正确的是 (
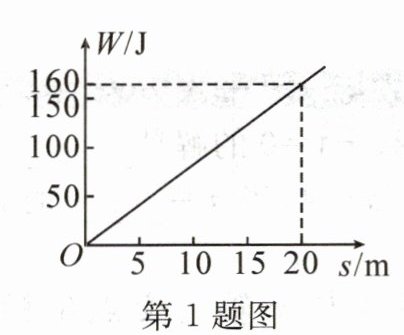
A. $ W = \frac{1}{8}s $
B. $ W = 20s $
C. $ W = 8s $
D. $ s = \frac{160}{W} $
C
)
A. $ W = \frac{1}{8}s $
B. $ W = 20s $
C. $ W = 8s $
D. $ s = \frac{160}{W} $
答案:
C
2. 一次函数 $ y = -x + b $ 的图象经过点 $ A(-1,6) $,则 $ b = $
5
。
答案:
5
3. 如图,一次函数的图象经过A,B两点,则这个函数的表达式为

$ y = 5x - 2 $
,点 $ P(-1,7) $不在
该一次函数的图象上(填“在”或“不在”)。
答案:
$ y = 5x - 2 $ 不在
4. 随着海拔的升高,大气压强下降,空气中的含氧量也随之下降,即含氧量 $ y(g/m^3) $ 与大气压强 $ x(kPa) $ 成正比例函数关系。当 $ x = 36 $ 时, $ y = 108 $,则含氧量 $ y(g/m^3) $ 与大气压强 $ x(kPa) $ 之间的关系式是
$ y = 3x $
。当大气压强是29kPa时,含氧量是87
$ g/m^3 $。
答案:
$ y = 3x $ 87
5. 在一次蜡烛燃烧实验中,蜡烛燃烧时剩余部分的高度 $ y(cm) $ 是燃烧时间 $ x(h) $ 的一次函数。蜡烛点燃前的高度为30cm,燃烧3h后,蜡烛剩余部分的高度为12cm。
(1)蜡烛燃烧时, $ y(cm) $ 与 $ x(h) $ 之间的关系式是
(2)蜡烛从点燃到燃尽所用的时间是
(1)蜡烛燃烧时, $ y(cm) $ 与 $ x(h) $ 之间的关系式是
$ y = -6x + 30 $
。(2)蜡烛从点燃到燃尽所用的时间是
5 h
。
答案:
(1) $ y = -6x + 30 $
(2) 5 h
(1) $ y = -6x + 30 $
(2) 5 h
6. 一次函数 $ y = kx + b $ 的图象经过点 $ A(2,3) $,每当x增加1个单位长度时,y增加3个单位长度,则此函数的表达式是
$ y = 3x - 3 $
。
答案:
$ y = 3x - 3 $
7. 如图,已知B中的实数与A中的实数之间的对应关系是某个一次函数。
(1)若用y表示B中的实数,用x表示A中的实数,求y与x之间的函数表达式。
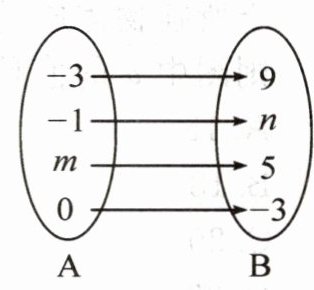
(2)求 $ m + n $ 的值。
(1) 设一次函数的表达式为 $ y = kx + b $。根据题意,得 $ -3 = b $,① $ 9 = -3k + b $。② 将①代入②,得 $ k = -4 $。∴ $ y $ 与 $ x $ 之间的函数表达式为 $ y = $
(2) 在 $ y = -4x - 3 $ 中,当 $ x = -1 $ 时,$ n = -4×(-1) - 3 = 1 $;当 $ y = 5 $ 时,$ -4m - 3 = 5 $,解得 $ m = -2 $。∴ $ m + n $ 的值为
(1)若用y表示B中的实数,用x表示A中的实数,求y与x之间的函数表达式。

(2)求 $ m + n $ 的值。
(1) 设一次函数的表达式为 $ y = kx + b $。根据题意,得 $ -3 = b $,① $ 9 = -3k + b $。② 将①代入②,得 $ k = -4 $。∴ $ y $ 与 $ x $ 之间的函数表达式为 $ y = $
$-4x - 3$
。(2) 在 $ y = -4x - 3 $ 中,当 $ x = -1 $ 时,$ n = -4×(-1) - 3 = 1 $;当 $ y = 5 $ 时,$ -4m - 3 = 5 $,解得 $ m = -2 $。∴ $ m + n $ 的值为
$-1$
。
答案:
解:
(1) 设一次函数的表达式为 $ y = kx + b $。根据题意,得 $ -3 = b $,① $ 9 = -3k + b $。② 将①代入②,得 $ k = -4 $。
∴ $ y $ 与 $ x $ 之间的函数表达式为 $ y = -4x - 3 $。
(2) 在 $ y = -4x - 3 $ 中,当 $ x = -1 $ 时,$ n = -4×(-1) - 3 = 1 $;当 $ y = 5 $ 时,$ -4m - 3 = 5 $,解得 $ m = -2 $。
∴ $ m $、$ n $ 的值分别为 -1,-2。
(1) 设一次函数的表达式为 $ y = kx + b $。根据题意,得 $ -3 = b $,① $ 9 = -3k + b $。② 将①代入②,得 $ k = -4 $。
∴ $ y $ 与 $ x $ 之间的函数表达式为 $ y = -4x - 3 $。
(2) 在 $ y = -4x - 3 $ 中,当 $ x = -1 $ 时,$ n = -4×(-1) - 3 = 1 $;当 $ y = 5 $ 时,$ -4m - 3 = 5 $,解得 $ m = -2 $。
∴ $ m $、$ n $ 的值分别为 -1,-2。
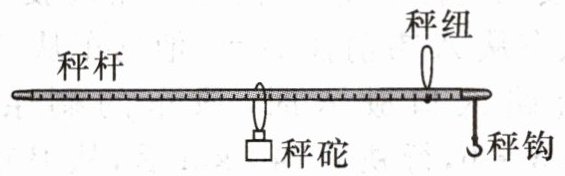
8. 新考向 传统文化 杆秤是我国传统的计重工具,如图,秤钩上所挂物体的质量不同,使得秤砣到秤纽的水平距离不同。称重时,秤钩所挂物重为 $ x(kg) $ 时,秤杆上秤砣到秤纽的水平距离为 $ y(cm) $。下表为若干次称重时所记录的一些数据,且y是x的一次函数。

注:秤杆上秤砣在秤纽左侧时,水平距离 $ y(cm) $ 为正,在右侧时为负。
(1)根据题意,完成上表。
(2)请求出y与x之间的关系式。
(3)当秤杆上秤砣到秤纽的水平距离为15cm时,秤钩所挂物重是____kg。
(1) 1.50 11
(2) 设 $ y $ 与 $ x $ 之间的关系式为 $ y = kx + b $。根据题意,得 $ -2 = b $,① $ 1 = 0.75k + b $。② 将①代入②,得 $ k = 4 $。
∴ $ y $ 与 $ x $ 之间的关系式为 $ y = 4x - 2 $。
(3) 4.25

注:秤杆上秤砣在秤纽左侧时,水平距离 $ y(cm) $ 为正,在右侧时为负。
(1)根据题意,完成上表。
(2)请求出y与x之间的关系式。
(3)当秤杆上秤砣到秤纽的水平距离为15cm时,秤钩所挂物重是____kg。

(1) 1.50 11
(2) 设 $ y $ 与 $ x $ 之间的关系式为 $ y = kx + b $。根据题意,得 $ -2 = b $,① $ 1 = 0.75k + b $。② 将①代入②,得 $ k = 4 $。
∴ $ y $ 与 $ x $ 之间的关系式为 $ y = 4x - 2 $。
(3) 4.25
答案:
解:
(1) 1.50 11
(2) 设 $ y $ 与 $ x $ 之间的关系式为 $ y = kx + b $。根据题意,得 $ -2 = b $,① $ 1 = 0.75k + b $。② 将①代入②,得 $ k = 4 $。
∴ $ y $ 与 $ x $ 之间的关系式为 $ y = 4x - 2 $。
(3) 4.25
(1) 1.50 11
(2) 设 $ y $ 与 $ x $ 之间的关系式为 $ y = kx + b $。根据题意,得 $ -2 = b $,① $ 1 = 0.75k + b $。② 将①代入②,得 $ k = 4 $。
∴ $ y $ 与 $ x $ 之间的关系式为 $ y = 4x - 2 $。
(3) 4.25
查看更多完整答案,请扫码查看


