《2025年名校课堂八年级数学上册北师大版》

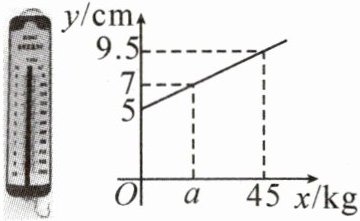
1. 如图,一个条形测力计不挂重物时长5cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比,弹簧总长y(cm)关于所挂物体质量x(kg)的函数图象如图所示,则图中a的值是(C)

A. 15
B. 18
C. 20
D. 33

答案： C

2. 由于持续高温和连日无雨,水库蓄水量普遍下降.如图所示的是某水库蓄水量V(万$m^3)$与干旱时间t(天)之间的关系图,请你根据此图填空：
(1)水库原蓄水量是1000万$m^3,$干旱持续10天,蓄水量为800万$m^3.$
(2)若水库的蓄水量小于400万$m^3$时,将发出严重干旱警报,则持续干旱30天后,将发出严重干旱警报.按此规律,持续干旱50天时,水库的水将干涸.

答案：
(1) 1000 800
(2) 30 50

3. 如果生产某种产品的成本y(万元)与产量x(吨)之间的关系如图所示,那么生产5吨这种产品所需的成本是10万元.

答案： 10

4. (2024·陕西)我国新能源汽车快速健康发展,续航里程不断提升,王师傅驾驶一辆纯电动汽车从A市前往B市.他驾车从A市一高速公路入口驶入时,该车的剩余电量是80kW·h,行驶了240km后,从B市一高速公路出口驶出.已知该车在高速公路上行驶的过程中,剩余电量y(kW·h)与行驶路程x(km)之间的关系如图所示.
(1)求y与x之间的关系式.$ y = -\frac{1}{5}x + 80 $
(2)已知这辆车的“满电量”为100kW·h,求王师傅驾车从B市这一高速公路出口驶出时,该车的剩余电量占“满电量”的百分之多少.32%

答案： 解:
(1) 设 $ y = kx + b $，根据题意，得 $ 80 = b $，① $ 50 = 150k + b $，②
将①代入②，得 $ k = -\frac{1}{5} $。$ \therefore y = -\frac{1}{5}x + 80 $。
(2) 令 $ x = 240 $，则 $ y = -\frac{1}{5}×240 + 80 = 32 $。$ \frac{32}{100}×100\% = 32\% $。答: 该车的剩余电量占“满电量”的 32%。

5. (1)一元一次方程-2x+4= 0的解是x = 2.
(2)已知函数y= -2x+4,当x= 2时,函数值y= 0.
(3)直线y= -2x+4与x轴的交点坐标是(2,0).
(4)由上述问题可知,一元一次方程ax+b= 0的解就是一次函数y= ax+b中当y= 0时所对应的x的值；从图象上看,就是一次函数y= ax+b的图象与x轴交点的横坐标.

答案：
(1) $ x = 2 $
(2) 2
(3) $ (2,0) $
(4) $ x $ $ x $ 横坐标

6. 已知关于x的方程kx+b= 0(k≠0)的解是x= 2,则一次函数y= kx+b(k≠0)的图象与x轴的交点坐标是(2,0).

答案： $ (2,0) $

7. 已知一次函数y= kx+b的图象如图所示,利用图象解决下列问题.
(1)关于x的方程kx+b= 0的解是x = 2.
(2)关于x的方程kx+b= 2的解是x = 1.
(3)关于x的方程kx+b= 4的解是x = 0.

答案：
(1) $ x = 2 $
(2) $ x = 1 $
(3) $ x = 0 $

8. 已知一次函数y= 2x+n的图象如图所示,则方程2x+n= 0的解可能是(C)

A. x= 1
B. x= 3/2
C. x= -3/5
D. x= -1

答案： C