第8页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 如图,从电线杆离地面 6 米处向地面拉一条 10 米长的钢缆,地面钢缆固定点 A 到电线杆底部 B 的距离 AB 是(
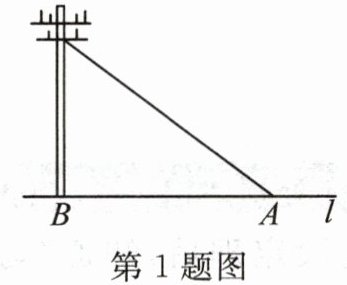
A. 6 米
B. 7 米
C. 8 米
D. 9 米
C
)
A. 6 米
B. 7 米
C. 8 米
D. 9 米
答案:
C
2. 如图,长方形阴影部分的面积是(
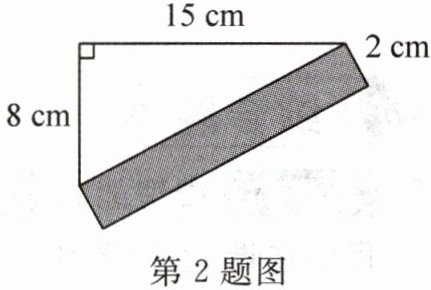
A. $16cm^{2}$
B. $17cm^{2}$
C. $30cm^{2}$
D. $34cm^{2}$
D
)
A. $16cm^{2}$
B. $17cm^{2}$
C. $30cm^{2}$
D. $34cm^{2}$
答案:
D
3. 若要将一块不能弯曲的正方形(厚度忽略不计)搬进室内,需要通过一扇如图所示的高为 2 m,宽为 1 m 的门,以下边长的木块中哪块可以通过此门(
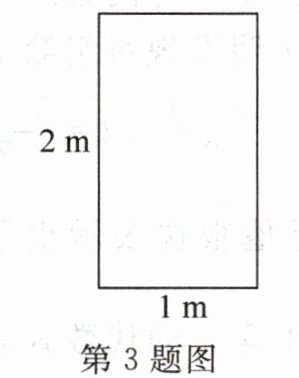
A. 2.8 m
B. 2.5 m
C. 2.2 m
D. 以上答案都不对
C
)
A. 2.8 m
B. 2.5 m
C. 2.2 m
D. 以上答案都不对
答案:
C
4. (教材 P14 随堂练习 T1 变式)有五根小木棒,其长度分别为 7,15,20,24,25,现将它们摆成两个直角三角形,其中正确的是(

C
)
答案:
C
5. A 石家庄外国语校本经典题 如图,在长方形 ABCD 中,$AB = 8$,$AD = 10$。将长方形 ABCD 沿直线 AF 折叠,使点 D 落在 BC 上的点 E 处,则 CE 的长为

4
。
答案:
4
6. 下图是 $5×9$ 的方格纸,每个小正方形的边长都是 1 cm,一只蚂蚁沿图中折线($A→B→C→D$)从点 A 爬到点 D,共爬行了
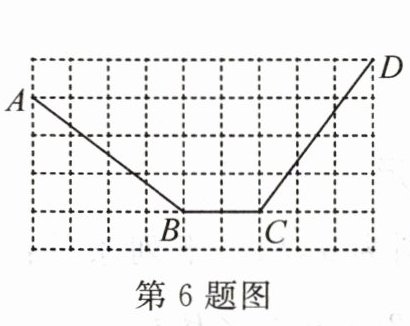
12
cm。
答案:
12
7. 如图,在离水面高度为 8 米的岸上,有人用绳子拉船靠岸,开始时绳子 BC 的长为 17 米,几分钟后船到达点 D 的位置,此时绳子 CD 的长为 10 米,则船向岸边移动了
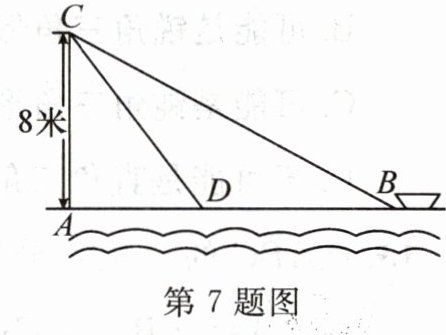
9
米。
答案:
9
8. (2024·吉林)图 1 中有一首古算诗,根据诗中的描述可以计算出红莲所在位置的湖水深度,其示意图如图 2,其中 $AB = AB'$,$AB⊥B'C$于点 C,$BC = 0.5$尺,$B'C = 2$尺。设 AC 的长度为 x 尺,可列方程为

$ x^{2}+2^{2}=(x + 0.5)^{2} $
。
答案:
$ x^{2}+2^{2}=(x + 0.5)^{2} $
9. 如图,$∠AOB = 90^{\circ}$,$OA = 18dm$,$OB = 6dm$,一机器人在点 B 处看见一个小球从点 A 出发沿着 AO 方向匀速滚向点 O,机器人立即从点 B 出发,沿直线匀速前进拦截小球,恰好在点 C 处截住了小球。如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程 BC 是

10
dm。
答案:
解:
∵小球滚动的速度与机器人行走的速度相等,运动时间相等,
∴ $ BC = AC $。设 $ AC = x \mathrm{dm} $,则 $ OC = (18 - x) \mathrm{dm} $。由勾股定理,得 $ OB^{2}+OC^{2}=BC^{2} $,即 $ 6^{2}+(18 - x)^{2}=x^{2} $。解得 $ x = 10 $。答:机器人行走的路程 $ BC $ 是 $ 10 \mathrm{dm} $。
∵小球滚动的速度与机器人行走的速度相等,运动时间相等,
∴ $ BC = AC $。设 $ AC = x \mathrm{dm} $,则 $ OC = (18 - x) \mathrm{dm} $。由勾股定理,得 $ OB^{2}+OC^{2}=BC^{2} $,即 $ 6^{2}+(18 - x)^{2}=x^{2} $。解得 $ x = 10 $。答:机器人行走的路程 $ BC $ 是 $ 10 \mathrm{dm} $。
查看更多完整答案,请扫码查看


