《2025年名校课堂八年级数学上册北师大版》

1. 估计68的立方根在(C)
A. 2和3之间
B. 3和4之间
C. 4和5之间
D. 5和6之间

答案： C

2. 若面积为10的正方形的边长为a,则a的值在(C)
A. 1和2之间
B. 2和3之间
C. 3和4之间
D. 4和5之间

答案： C

3. 新考向 开放性问题(2024·广西)写出一个比$\sqrt{3}$大的整数：2（答案不唯一）.

答案： 2（答案不唯一）

4. 比较下列各数的大小(填“＞”“＜”或“＝”)：
(1)(2024·山西)$\sqrt{6}$＞2.
(2)－2.3＜$-\sqrt{5}$.
(3)$\frac{\sqrt{7}-1}{3}$＜$\frac{2}{3}$.

答案：
(1) ＞
(2) ＜
(3) ＜

5. A|石家庄外国语校本经典题 有A,B两个底面均为正方形的长方体,长方体A的高为8,体积为27,长方体B的高为6,体积为24.比较这两个长方体的底面边长的大小.

答案： 解：设长方体 A 的底面边长为 x。依题意，得 $8x^{2}=27$，$\therefore x=\sqrt{\frac{27}{8}}$。设长方体 B 的底面边长为 y。依题意，得 $6y^{2}=24$，$\therefore y = 2$。$\because \frac{27}{8}＜4$，$\therefore \sqrt{\frac{27}{8}}＜\sqrt{4}$，即 $\sqrt{\frac{27}{8}}＜2$。$\therefore$ 长方体 A 的底面边长小于长方体 B 的底面边长。

6. 利用计算器求下列各式的值(结果精确到0.01)：
(1)$\sqrt{867}$≈29.44. (2)$-\sqrt[3]{\frac{8}{25}}$≈-0.68.

答案：
(1)29.44
(2)-0.68

7. 利用计算器比较下列各组数的大小：
(1)$\sqrt[3]{11}$＜$\sqrt{5}$. (2)$\frac{5}{8}$＞$\frac{\sqrt{5}-1}{2}$.

答案：
(1) ＜
(2) ＞

8. 若$a= \sqrt[3]{7}$,$b= \sqrt{5}$,$c= 2$,则a,b,c的大小关系为(C)
A. $b＜c＜a$
B. $b＜a＜c$
C. $a＜c＜b$
D. $a＜b＜c$

答案： C

9. A|人大附中校本经典题 写出所有符合下列条件的数：
(1)小于$\sqrt{37}$的所有正整数：1,2,3,4,5,6.
(2)大于$-\sqrt{10}且小于\sqrt{10}$的所有整数：-3,-2,-1,0,1,2,3.
(3)绝对值小于$\sqrt{6}$的所有整数：-2,-1,0,1,2.

答案：
(1)1,2,3,4,5,6
(2)-3,-2,-1,0,1,2,3
(3)-2,-1,0,1,2

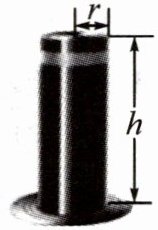
10. A|清华附中校本经典题 如图,这是一种圆柱形升降阻车桩,它的体积为22600$\mathrm{cm}^3$,高h等于底面半径r的5.48倍,则底面半径r是10.95厘米？(π取3.14,结果精确到0.01 cm)

答案： 解：根据题意，得 $\pi r^{2}h = 22600$，又 $\because h = 5.48r$，$\therefore \pi r^{2}\cdot 5.48r = 22600$，即 $17.2072r^{3}=22600$，解得 $r\approx 10.95$。答：底面半径 r 大约是 10.95 cm。

11. 新考向 阅读理解 阅读下面的材料,解答问题：
我们知道,$\sqrt{2}$是无理数,而无理数是无限不循环小数,因此$\sqrt{2}$的小数部分我们不可能全部写出来,于是小明用$\sqrt{2}-1来表示\sqrt{2}$的小数部分.你同意小明的表示方法吗？
事实上,小明的表示方法是有道理的,因为$\sqrt{2}$的整数部分是1,将$\sqrt{2}$减去其整数部分,差就是小数部分.
又例如：
∵$\sqrt{4}＜\sqrt{7}＜\sqrt{9}$,即$2＜\sqrt{7}＜3$,
∴$\sqrt{7}$的整数部分为2,小数部分为$\sqrt{7}-2$.
请解答：
(1)$\sqrt{17}$的整数部分是4,小数部分是$\sqrt{17}-4$.
(2)若a是$\sqrt{70}$的整数部分,b是$\sqrt{5}$的小数部分,求$a+b-\sqrt{5}+3$的平方根.
解：$\because \sqrt{64}＜\sqrt{70}＜\sqrt{81}$，即 $8＜\sqrt{70}＜9$，$\therefore \sqrt{70}$ 的整数部分为 8，即 $a = 8$。$\because \sqrt{4}＜\sqrt{5}＜\sqrt{9}$，即 $2＜\sqrt{5}＜3$，$\therefore \sqrt{5}$ 的整数部分为 2，小数部分为 $\sqrt{5}-2$，即 $b=\sqrt{5}-2$。$\therefore a + b-\sqrt{5}+3 = 8+\sqrt{5}-2-\sqrt{5}+3 = 9$。$\because 9$的平方根为$\pm 3$，$\therefore a + b-\sqrt{5}+3$ 的平方根为 $\pm 3$。

答案： 解：
(1)4 $\sqrt{17}-4$
(2) $\because \sqrt{64}＜\sqrt{70}＜\sqrt{81}$，即 $8＜\sqrt{70}＜$9，$\therefore \sqrt{70}$ 的整数部分为 8，即 $a = 8$。$\because \sqrt{4}＜\sqrt{5}＜\sqrt{9}$，即 $2＜\sqrt{5}＜3$，$\therefore \sqrt{5}$ 的整数部分为 2，小数部分为 $\sqrt{5}-2$，即 $b=\sqrt{5}-2$。$\therefore a + b-\sqrt{5}+3 = 8+\sqrt{5}-2-\sqrt{5}+3 = 9$。$\because \sqrt{9}=\pm 3$，$\therefore a + b-\sqrt{5}+3$ 的平方根为 $\pm 3$。