《2025年名校课堂八年级数学上册北师大版》

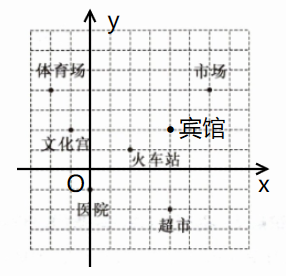
7. 如图,已知火车站的坐标为$(2,1)$,文化宫的坐标为$(-1,2).$
(1)请根据题目条件画出平面直角坐标系.（图略）
(2)写出体育场、市场、超市的坐标.体育场$(-2,4)$，市场$(6,4)$，超市$(4,-2)$.
(3)若宾馆的坐标为$(4,2)$,请在图上标出宾馆所在位置.（图略）

答案：
解: 
(2) 体育场(−2,4), 市场(6,4), 超市(4,−2).
(1)
(3) 如图

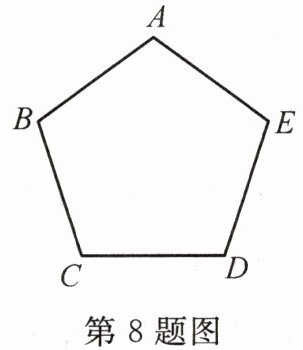
8. 如图,将正五边形ABCDE放入某平面直角坐标系中.若顶点A,B,C,D的坐标分别是$(0,a),(-3,2),(b,m),(c,m)$,则点E的坐标是 (C)

A.$(2,-3)$
B.$(2,3)$
C.$(3,2)$
D.$(3,-2)$

答案： C

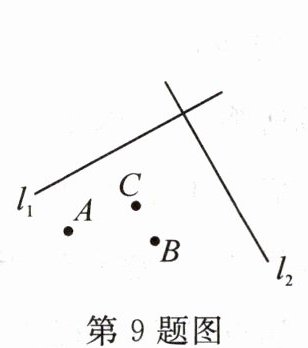
9. 如图,直线$l_{1}⊥l_{2}$,在平面直角坐标系中,$l_{1}// x$轴,$l_{2}// y$轴,点A,B的坐标分别为$(-1,1),(2,-1)$,则点C在第一象限内.

答案： 一

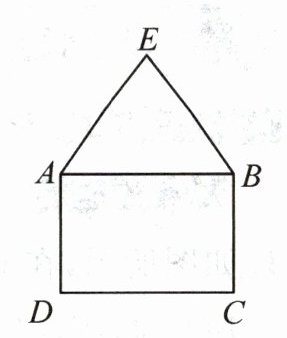
10. 新考向 开放性问题 如图所示,在长方形ABCD中,已知$AB= 6,AD= 4$,在长方形ABCD外画$△ABE$,使$AE= BE= 5$,请建立适当的平面直角坐标系,并求出各顶点的坐标.

解: 以点 D 为坐标原点, DC 所在直线为 x 轴, AD 所在直线为y 轴, 建立平面直角坐标系, 则 $A(0,4),B(6,4),C(6,0),D(0,0)$. 过点 E 作 $EG \perp CD$ 于点 G, 交 AB 于点 F, 则 $\angle AFE = 90^{\circ}$.$\because AE = BE, \therefore AF = \frac{1}{2}AB = \frac{1}{2} × 6 = 3$. 在 $Rt \triangle AEF$ 中, $EF = \sqrt{AE^2 - AF^2} = \sqrt{5^2 - 3^2} = 4. \therefore EG = 4 + 4 = 8. \therefore E(3,8)$. (答案不唯一)

答案： 解: 以点 D 为坐标原点, DC 所在直线为 x 轴, AD 所在直线为y 轴, 建立平面直角坐标系, 则 $A(0,4),B(6,4),C(6,0),D(0,0)$. 过点 E 作 $EG \perp CD$ 于点 G, 交 AB 于点 F, 则 $\angle AFE = 90^{\circ}$.
$\because AE = BE, \therefore AF = \frac{1}{2}AB = \frac{1}{2} \times 6 = 3$. 在 $Rt \triangle AEF$ 中, $EF = \sqrt{AE^2 - AF^2} = \sqrt{5^2 - 3^2} = 4. \therefore EG = 4 + 4 = 8. \therefore E(3,8)$. (答案不唯一)

11. A|北京四中校本经典题 在某研学活动中,主办方告诉学员们A,B两点的位置及坐标分别为$(-3,1),(-2,-3)$,同时只告诉学员们活动中心C的坐标为$(3,2)$.(单位:km)
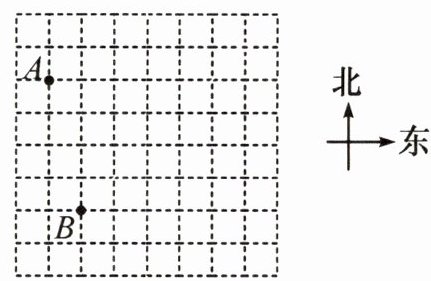
(1)请在图中建立平面直角坐标系,并确定点C的位置.图略
(2)若学员们打算从点B处直接赶往点C处,请用方位角和距离描述点C相对于点B的位置.点 C 在点 B 的北偏东 $45^{\circ}$ 方向上, 距离点 B $5\sqrt{2} km$ 处

答案：
解:
(1) 
 
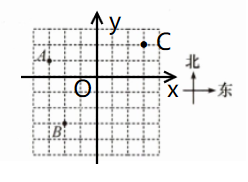
(2) 点 C 在点 B 的北偏东 $45^{\circ}$ 方向上, 距离点 B $5\sqrt{2} km$ 处.

12. 勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直的铁路经过A,B两地.
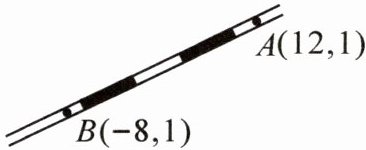
(1)A,B间的距离为20km.
(2)计划修一条从C地到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C两地的距离相等,则C,D间的距离为13km.

答案：
(1) 20
(2) 13