《2025年节节高大象出版社八年级数学上册华师大版》

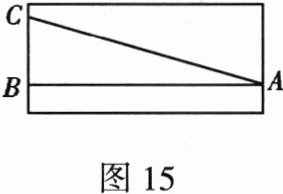
18. （9分）如图15，某游泳池长48 m，小方和小杨进行游泳比赛，从同一处（点A）出发，小方的平均速度为3 m/s，小杨的平均速度为3.1 m/s，但小杨一心图快，不看方向沿斜线（AC方向）游，而小方沿直线（AB方向）游，两人到达终点的位置相距14 m，按各自的平均速度计算，谁先到达终点？为什么？

答案： 18. 解:小方先到达终点.理由如下:
由题意可知,AB=48m,BC=14m,
在Rt△ABC中，
∵　AC= $\sqrt{AB^2 + BC^2} = \sqrt{48^2 + 14^2} = 50$(m),
∴　小方用时48÷3=16(s)，
小杨用时50÷3.1=16$\frac{4}{31}$(s).
∵　16＜16$\frac{4}{31}$,
∴小方用时少，即小方先到达终点.

19. （9分）公路旁有一块山地正在开发，现在点C处需要爆破，已知点C与公路上的停靠站A的距离为300 m，与公路上另一停靠站B的距离为400 m，且$CA \perp CB$，如图16. 为了安全起见，爆破点C周围半径250 m范围内不得进入，问：在进行爆破时，公路AB段是否有危险？是否需要暂时封锁？请通过计算进行说明.

答案：
19. 解:如图,过点C作CD⊥AB于点D,
　　　　
∵　BC=400m,AC=300m,∠ACB=90°,
∴ 根据勾股定理得AB=500m.
∵　$\frac{1}{2}$AB·CD=$\frac{1}{2}$BC·AC,
∴　CD=240m.
∵　240m＜250m,
因此公路AB段需要暂时封锁.

20. （9分）如图17，某小区有两个喷泉A、B，两个喷泉的距离为250 m. 现要为喷泉铺设供水管道AM、BM，供水点M在小路AC上，供水点M到AB的距离MN的长为120 m，BM的长为150 m.
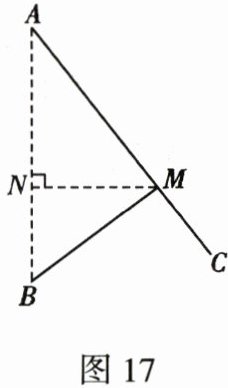
（1）求供水点M到喷泉A、B需要铺设的管道总长；
（2）求喷泉B到小路AC的最短距离.

答案： 20. 解:
(1)在Rt△MNB中,BN = $\sqrt{BM^2 - MN^2} = \sqrt{150^2 - 120^2} = 90$(m),
∴　AN=AB−BN=250−90=160(m).
在Rt△AMN中,AM = $\sqrt{AN^2 + MN^2} = \sqrt{160^2 + 120^2} = 200$(m),
∴　供水点M到喷泉A、B需要铺设的管道总长=AM+BM=200+150=350(m).
(2)
∵　AB=250m,AM=200m,BM=150m,
∴　AB²=BM²+AM²,
∴　△ABM是直角三角形，
∴　BM⊥AC,
∴　喷泉B到小路AC的最短距离是BM=150m.