《2025年节节高大象出版社八年级数学上册华师大版》

22. (10 分)如图 9，在$Rt\triangle ABC$中，$\angle B = 90^{\circ}$，$AD$平分$\angle BAC$。在小智他们刚学完“三角形全等的判定”这节课后，老师给出了一个富有挑战性的题目：利用所学知识推导出$\triangle ABD$和$\triangle ACD$面积的比值与边$AB$和$AC$长度的比值之间的关系。经过小组讨论，他们的总体思路是控制变量法，即过点$D$作$AC$的垂线，垂足为点$E$，再根据三角形全等来证明$\triangle ABD$和$\triangle ACD$的高相等，从而得到结论。请根据小智他们的思路完成以下作图与填空：

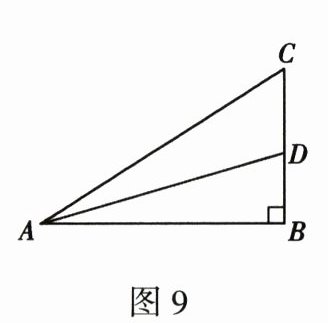
(1)尺规作图：过点$D$作$AC$的垂线，交$AC$于点$E$(不写作法，保留作图痕迹)。
(2)证明：$\because AD$平分$\angle BAC$，
$\therefore$ ①$∠DAE = ∠DAB$。
$\because DE\perp AC$，
$\therefore \angle AED=\angle B = 90^{\circ}$。
又②$AD = AD$，
$\therefore \triangle ABD\cong\triangle AED(AAS)$，
$\therefore$ ③$DE = DB$。
$\because S_{\triangle ABD}=\frac{1}{2}AB· DB$，$S_{\triangle ACD}=\frac{1}{2}AC· DE$，
$\therefore \frac{S_{\triangle ABD}}{S_{\triangle ACD}}=\frac{AB}{AC}$。
小智他们再进一步研究发现，只要一个三角形被其任意一内角的角平分线分为两个三角形，均有此结论。请你依照题意完成下面命题：
如果一个三角形满足被其任意一内角的平分线分为两个三角形，那么这两个三角形面积的比值与该角对应的两边长度的比值④相等。请用别的方法证明这个结论是真命题。

答案：
22.
(1)解：如图，$DE$即为所求。
　　　　　　
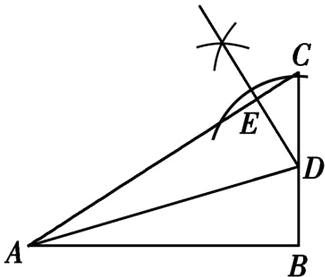
(2)证明：
∵$AD$平分$∠BAC$，
∴①$∠DAE = ∠DAB$。
∵$DE⊥AC$，
∴$∠AED = ∠B = 90°$。
　又②$AD = AD$，
∴$\triangle ABD\cong\triangle AED(AAS)$，
∴③$DE = DB$。
∵$S_{\triangle ABD} = \frac{1}{2}AB· DB$，$S_{\triangle ACD} = \frac{1}{2}AC· DE$，
∴$\frac{S_{\triangle ABD}}{S_{\triangle ACD}} = \frac{AB}{AC}$。
已知，任意$\triangle ABC$中，$AD$平分$∠BAC$，过点$D$作$DE⊥AC$于点$E$，$DF⊥AB$于点$F$，如图所示，
　　　　　　
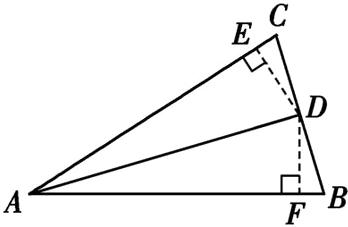
则$∠AED = ∠AFD = 90°$，
∵$AD$平分$∠BAC$，
∴$∠DAE = ∠DAF$。
∵$AD = AD$，
∴$\triangle AED\cong\triangle AFD(AAS)$，
∴$DE = DF$。
∵$S_{\triangle ABD} = \frac{1}{2}AB· DF$，$S_{\triangle ACD} = \frac{1}{2}AC· DE$，
∴$\frac{S_{\triangle ABD}}{S_{\triangle ACD}} = \frac{AB}{AC}$。
∴如果一个三角形满足被其任意一内角角平分线分为两个三角形，那么这两个三角形面积的比值与该角对应的两边长度的比值④相等。
证明略。