《2025年节节高大象出版社八年级数学上册华师大版》

6. 某校为了扩建劳动实践基地，准备在长、宽如图 1 所示的长方形空地上修建横、纵宽度均为 $a$ m 的三条小路(阴影部分)，其余部分(即空白部分)作为劳动实践基地. 则劳动实践基地的总面积是$(2a+2b)(a+4b)$ $m^2$.

答案： 6.$(2a+2b)(a+4b)$

7. 化简：
(1) $2(2x^2 - xy) + x(x - y)$；
(2) $ab(2ab^2 - a^2b) - (2ab)^2b + a^3b^2$.

答案： 7.
(1)$2(2x^{2}-xy)+x(x-y)$
$=4x^{2}-2xy+x^{2}-xy$
$=5x^{2}-3xy$.
(2)$ab(2ab^{2}-a^{2}b)-(2ab)^{2}b+a^{3}b^{2}$
$=2a^{2}b^{3}-a^{3}b^{2}-4a^{2}b^{3}+a^{3}b^{2}$
$=-2a^{2}b^{3}$.

8. 计算：
(1) $(2x + 3)(-x - 1)$；
(2) $(2m - 1)(3m - 2)$；
(3) $x(y - x) - y(x - y)$.

答案： 8.解：
(1)原式$=-2x^{2}-2x-3x-3=-2x^{2}-5x-3$.
(2)原式$=6m^{2}-4m-3m+2=6m^{2}-7m+2$.
(3)原式$=xy-x^{2}-xy+y^{2}=-x^{2}+y^{2}$.

9. 【实践教学】
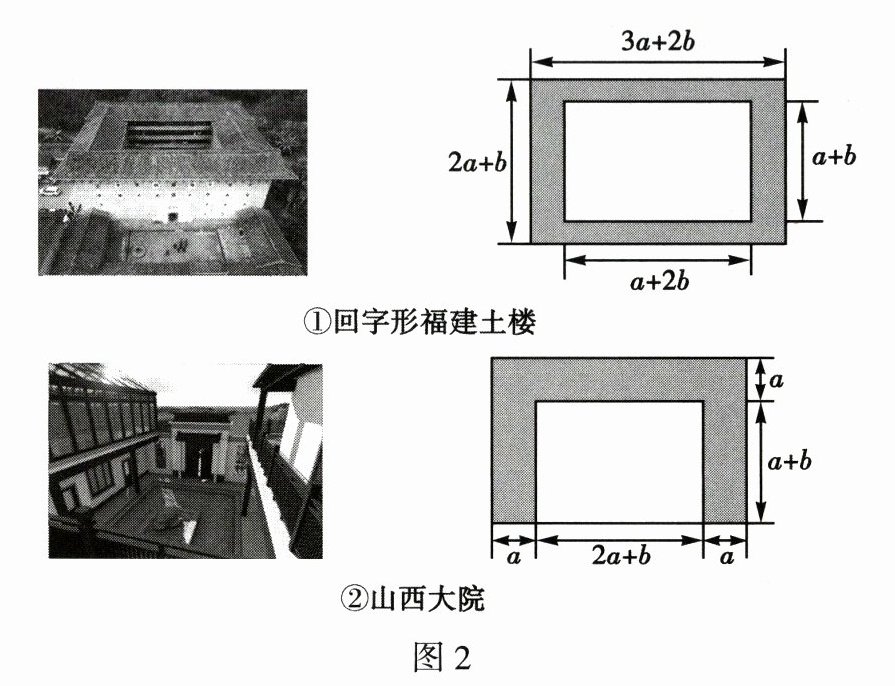
某校同学在社会实践的过程中，遇到了一些各具特色的建筑，有在世界遗产大会上被正式列入《世界遗产名录》的福建土楼，也有被誉为中国民居建筑典范的山西大院，同学们对于哪个建筑的占地面积(图 2 中阴影)更大展开了讨论.
①组的同学认为图 2①中回字形福建土楼的占地面积更大；
②组的同学认为图 2②中山西大院的占地面积更大.
【数据采集】
为了证明自己的想法是正确的，两组同学分别对建筑物进行了数据测量，数据如图所示.
【数据应用】
(1) 请分别计算这两个建筑物的占地面积；
(2) 若 $0 ＜ a ＜ b$，则①组同学的想法正确. (填“①”或“②”)

答案： 9.解：
(1)回字形福建土楼占地面积为
$(3a+2b)(2a+b)-(a+2b)(a+b)$
$=6a^{2}+3ab+4ab+2b^{2}-a^{2}-ab-2ab-2b^{2}$
$=5a^{2}+4ab$,
山西大院占地面积为
$(a+a+b)(2a+b+a+a)-(2a+b)(a+b)$
$=(2a+b)(4a+b)-(2a+b)(a+b)$
$=(2a+b)(4a+b-a-b)$
$=(2a+b)·3a=6a^{2}+3ab$.
(2)①【解析】这两个建筑物的占地面积之差为
$5a^{2}+4ab-6a^{2}-3ab$
$=-a^{2}+ab=a(b-a)$,
$\because0＜a＜b$,
$\therefore a(b-a)＞0$,
$\therefore$回字形福建土楼的占地面积更大,
即①组同学的想法正确.